Câu hỏi:
2 năm trước
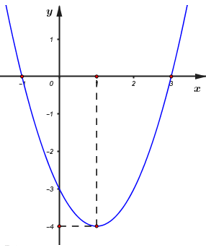
Cho parabol $\left( P \right):y = a{x^2} + bx + c$$\left( {a \ne 0} \right)$ có đồ thị như hình bên. Tìm các giá trị $m$ để phương trình $\left| {a{x^2} + bx + c} \right| = m$ có bốn nghiệm phân biệt.
Trả lời bởi giáo viên
Đáp án đúng: b
Quan sát đồ thị ta có đồ thị hàm số \(y = \left| {a{x^2} + bx + c} \right|\) là là phần đồ thị phía trên trục hoành của $\left( P \right)$ và phần có được do lấy đối xứng phần phía dưới trục hoành của $\left( P \right)$, như hình vẽ sau:
Phương trình $\left| {a{x^2} + bx + c} \right| = m$ có bốn nghiệm phân biệt khi đường thẳng $y = m$ cắt đồ thị hàm số hàm số $y = \left| {a{x^2} + bx + c} \right|$ tại bốn điểm phân biệt.
Suy ra \(0 < m < 3\).
Hướng dẫn giải:
Dựng đồ thị hàm số \(y = \left| {f\left( x \right)} \right|\) từ đồ thị hàm số \(y = f\left( x \right)\) bằng cách giữ nguyên phần đồ thị phía trên \(Ox\) và lấy đối xứng phần dưới qua \(Ox\) rồi xóa phần dưới cũ đi.
