Câu hỏi:
2 năm trước
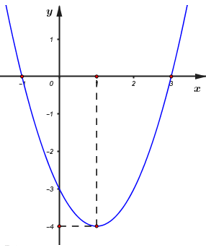
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình bên. Có bao nhiêu giá trị \(m\) nguyên để phương trình \(\left| {f\left( x \right) + 1} \right| = m\) có 4 nghiệm phân biệt?
Trả lời bởi giáo viên
Đáp án đúng: c
Phương trình \(\left| {f\left( x \right) + 1} \right| = m\) có 4 nghiệm phân biệt \( \Leftrightarrow \left( P \right):y = \left| {f\left( x \right) + 1} \right|\) và đường thẳng \(d:y = m\) cắt nhau tại 4 điểm phân biệt
\(\left( P \right):y = \left| {f\left( x \right) + 1} \right|\) có được bằng cách
Bước 1: Dịch đồ thị lên trên 1 đơn vị
Bước 2: Giữ nguyên phần nằm trên đồ thị; lấy đối xứng phần nằm dưới đồ thị qua Ox
Bước 3: Gạch bỏ phần nằm dưới trục \(Ox\)
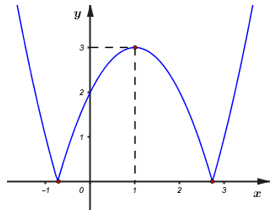
Dựa vào đồ thị hàm số ta thấy: đường thẳng \(d:\,\,y = m\) cắt đồ thị hàm số \(y = \left| {f\left( x \right) + 1} \right|\) tại \(4\) điểm phân biệt \( \Leftrightarrow 0 < m < 3\)
Lại có: \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {1;2} \right\} \Rightarrow \) có 2 giá trị \(m\) thỏa mãn bài toán.
Hướng dẫn giải:
Phương trình \(\left| {f\left( x \right) + 1} \right| = m\) có 4 nghiệm phân biệt \( \Leftrightarrow \left( P \right):y = \left| {f\left( x \right) + 1} \right|\) và đường thẳng \(d:y = m\) cắt nhau tại 4 điểm phân biệt
