Hỏi có bao nhiêu giá trị $m$ nguyên trong nửa khoảng $\left( {0;2017} \right]$ để phương trình $\left| {{x^2} - 4} \right|x\left| { - 5} \right| - m = 0$ có hai nghiệm phân biệt?
Trả lời bởi giáo viên
PT: $\left| {{x^2} - 4} \right|x\left| { - 5} \right| - m = 0 \Leftrightarrow \left| {{x^2} - 4} \right|x\left| { - 5} \right| = m\left( 1 \right)$
Số nghiệm phương trình \(\left( 1 \right) \) bằng số giao điểm của đồ thị hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\,\left( P \right)\) và đường thẳng \(y = m\) (cùng phương \(Ox\)).
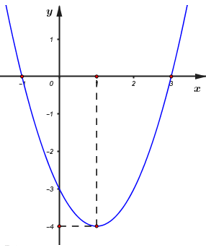
Xét hàm số \(y = {x^2} - 4x - 5\,\,\left( {{P_1}} \right)\) có đồ thị như hình 1.

Xét hàm số \(y = {x^2} - 4\left| x \right| - 5\,\,\left( {{P_2}} \right)\) là hàm số chẵn nên có đồ thị nhận \(Oy\) làm trục đối xứng. Mà \(y = {x^2} - 4\left| x \right| - 5 = {x^2} - 4x - 5\) nếu \(x \ge 0\). Suy ra đồ thị hàm số \(\left( {{P_2}} \right)\) gồm hai phần:
+) Phần \(1\): Giữ nguyên đồ thị hàm số \(\left( {{P_1}} \right)\) phần bên phải \(Oy\).
+) Phần \(2\): Lấy đối xứng phần \(1\) qua trục \(Oy\).
Ta được đồ thị \(\left( {{P_2}} \right)\) như hình 2.
Xét hàm số \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\,\left( P \right)\), ta có: \(y = \left\{ \begin{array}{l}{x^2} - 4\left| x \right| - 5\,\,\,\,\,\,\,\,\,\,\left( {y \ge 0} \right)\\ - \left( {{x^2} - 4\left| x \right| - 5} \right)\,\,\left( {y < 0} \right)\end{array} \right.\).
Suy ra đồ thị hàm số \(\left( P \right)\) gồm hai phần:
+) Phần \(1\): Giữ nguyên đồ thị hàm số \(\left( {{P_2}} \right)\) phần trên \(Ox\).
+) Phần \(2\): Lấy đối xứng đồ thị hàm số \(\left( {{P_2}} \right)\) phần dưới \(Ox\) qua trục \(Ox\).
Ta được đồ thị \(\left( P \right)\) như hình 3.
Quan sát đồ thị hàm số \(\left( P \right)\) ta có:
Để $\left| {{x^2} - 4} \right|x\left| { - 5} \right| = m\,\,\,\left( 1 \right)$ có hai nghiệm phân biệt\( \Leftrightarrow \left[ \begin{array}{l}m > 9\\m = 0\end{array} \right.\).
Mà \(\left\{ \begin{array}{l}m \in \mathbb{Z}\\m \in \left( {0;\,2017} \right]\end{array} \right. \) \(\Rightarrow m \in \left\{ {10;\,11;\,12;\,...;\,2017} \right\}\).
Vậy có $2008$ giá trị của $m$ thỏa mãn.
Hướng dẫn giải:
- Dựng đồ thị hàm số \(y = {x^2} - 4x - 5\) trên mặt phẳng tọa độ, từ đó suy ra đồ thị các hàm số \(y = {x^2} - 4\left| x \right| - 5\) và \(y = \left| {{x^2} - 4\left| x \right| - 5} \right|\)
- Số nghiệm của phương trình là số giao điểm của đồ thị hàm số vẽ được với đường thẳng \(y = m\)