Câu hỏi:
2 năm trước
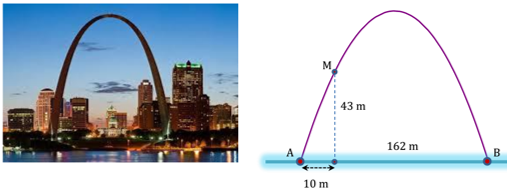
Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol (hình vẽ). Biết khoảng cách giữa hai chân cổng bằng \(162\,{\rm{m}}\). Trên thành cổng, tại vị trí có độ cao \(43\,{\rm{m}}\) so với mặt đất (điểm \(M\)), người ta thả một sợi dây chạm đất (dây căng thẳng theo phương vuông góc với đất). Vị trí chạm đất của đầu sợi dây này cách chân cổng A một đoạn \(10\,{\rm{m}}\). Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch (tính từ mặt đất đến điểm cao nhất của cổng).
Trả lời bởi giáo viên
Đáp án đúng: d
Chọn hệ trục tọa độ \(Oxy\) như hình vẽ.
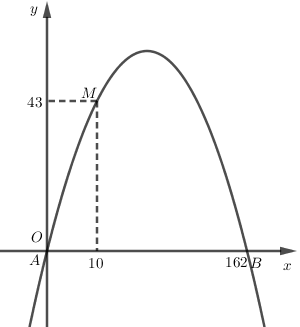
Phương trình Parabol \(\left( P \right)\) có dạng \(y = a{x^2} + bx + c\).
Parabol \(\left( P \right)\) đi qua điểm \(A\left( {0;0} \right)\), \(B\left( {162;0} \right)\), \(M\left( {10;43} \right)\) nên ta có
\(\left\{ \begin{array}{l}c = 0\\{162^2}a + 162b + c = 0\\{10^2}a + 10b + c = 43\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}c = 0\\a = - \dfrac{{43}}{{1520}}\\b = \dfrac{{3483}}{{760}}\end{array} \right.\)\( \Rightarrow \left( P \right):y = - \dfrac{{43}}{{1520}}{x^2} + \dfrac{{3483}}{{760}}x\).
Do đó chiều cao của cổng là \(h = - \dfrac{\Delta }{{4a}}\)\( = - \dfrac{{{b^2} - 4ac}}{{4a}}\)\( \approx 185,6m.\)
Hướng dẫn giải:
- Chọn hệ trục tọa độ \(Oxy\) với \(O \equiv A\), tia \(Ox\) cùng hướng tia \(OB\) và \(Oy\) hướng lên.
- Lập phương trình parabol rồi suy ra tọa độ đỉnh, tung độ đỉnh chính là chiều cao của cổng.
