Phương trình $\dfrac{{x - m}}{{x + 1}} = \dfrac{{x - 2}}{{x - 1}}$ có nghiệm duy nhất khi :
Điều kiện: $\left\{ \begin{array}{l}x \ne 1\\x \ne - 1\end{array} \right.$
Phương trình \(\left( 1 \right)\) thành
$\dfrac{{x - m}}{{x + 1}} = \dfrac{{x - 2}}{{x - 1}}\;\;\left( 1 \right)$$ \Leftrightarrow \left( {x - m} \right)\left( {x - 1} \right) = \left( {x - 2} \right)\left( {x + 1} \right)$$ \Leftrightarrow {x^2} - x - mx + m = {x^2} - x - 2$$ \Leftrightarrow mx = m + 2\,\,\,\left( 2 \right)$
Phương trình \(\left( 1 \right)\) có nghiệm duy nhất
\( \Leftrightarrow \) Phương trình \(\left( 2 \right)\) có nghiệm duy nhất khác \( - 1\) và \(1\)
\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\\dfrac{{m + 2}}{m} \ne 1\\\dfrac{{m + 2}}{m} \ne - 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m + 2 \ne m\\m + 2 \ne - m\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\2 \ne 0\;\;\left( {ld} \right)\\m \ne - 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne - 1\end{array} \right.\).
Biết phương trình $x - 2 + \dfrac{{x + a}}{{x - 1}} = a$ có nghiệm duy nhất và nghiệm đó là nghiệm nguyên. Vậy nghiệm đó là:
Điều kiện: $x \ne 1$
Phương trình \(\left( 1 \right)\) thành:
$x - 2 + \dfrac{{x + a}}{{x - 1}} = a$ $ \Leftrightarrow {x^2} - 3x + 2 + x + a = ax - a$$ \Leftrightarrow {x^2} - \left( {2 + a} \right)x + 2a + 2 = 0\,\,\,\,\left( 2 \right)$
Phương trình \(\left( 1 \right)\) có nghiệm duy nhất.
\( \Leftrightarrow \) Phương trình \(\left( 2 \right)\) có nghiệm duy nhất khác \(1\) hoặc phương trình \(\left( 2 \right)\) có $2$ nghiệm phân biệt có một nghiệm bằng \(1\)
\( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}\Delta = 0\\x = - \dfrac{b}{{2a}} \ne 1\end{array} \right.\\\left\{ \begin{array}{l}\Delta > 0\\f\left( 1 \right) = 0\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{a^2} - 4a - 4 = 0\\\dfrac{{a + 2}}{2} \ne 1\end{array} \right.\\\left\{ \begin{array}{l}{a^2} - 4a - 4 > 0\\1 - 2 - a + 2a + 2 = 0\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{a^2} - 4a - 4 = 0\\a + 2 \ne 2\end{array} \right.\\\left\{ \begin{array}{l}{a^2} - 4a - 4 > 0\\a + 1 = 0\end{array} \right.\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}a = 2 + 2\sqrt 2 \\a = 2 - 2\sqrt 2 \\a = - 1\end{array} \right.\)
Với \(a = 2 + 2\sqrt 2 \) phương trình có nghiệm là \(x = 2 + \sqrt 2 \)
Với \(a = 2 - 2\sqrt 2 \) phương trình có nghiệm là \(x = 2 - \sqrt 2 \)
Với \(a = - 1\) phương trình có nghiệm là \(\left[ \begin{array}{l}x = 0\;\;\left( n \right)\\x = 1\;\;\left( l \right)\end{array} \right.\)
Phương trình \(\left| {ax + b} \right| = \left| {cx + d} \right|\) tương đương với phương trình:
Ta có: \(\left| {ax + b} \right| = \left| {cx + d} \right| \Leftrightarrow \left[ \begin{array}{l}ax + b = cx + d\\ax + b = - cx - d\end{array} \right.\)
Tập nghiệm của phương trình:\(\left| {x - 2} \right| = \left| {3x - 5} \right|\)(1) là tập hợp nào sau đây ?
Ta có
$\left| {x - 2} \right| = \left| {3x - 5} \right|$$ \Leftrightarrow \left[ \begin{array}{l}x - 2 = 3x - 5\\x - 2 = 5 - 3x\end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}2x = 3\\4x = 7\end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{3}{2}\\x = \dfrac{7}{4}\end{array} \right.$.
Phương trình \(\left| {2x - 4} \right| + \left| {x - 1} \right| = 0\) có bao nhiêu nghiệm ?
Ta có
\(\left| {2x - 4} \right| + \left| {x - 1} \right| = 0\)\( \Leftrightarrow \left\{ \begin{array}{l}2x - 4 = 0\\x - 1 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\x = 1\end{array} \right.\;\;\left( {vl} \right)\)
Suy ra \(S = \emptyset \).
Phương trình \(\left| {2x - 4} \right| - 2x + 4 = 0\) có bao nhiêu nghiệm ?
Ta có: \(\left| {2x - 4} \right| - 2x + 4 = 0\)\( \Leftrightarrow \left| {2x - 4} \right| = 2x - 4\)\( \Leftrightarrow 2x - 4 \ge 0\)\( \Leftrightarrow x \ge 2\).
Tập nghiệm của phương trình $\dfrac{{x - 1}}{{2x - 3}} = \dfrac{{ - 3x + 1}}{{\left| {x + 1} \right|}}$\(\left( 1 \right)\) là :
Điều kiện: \(\left\{ \begin{array}{l}2x - 3 \ne 0\\\left| {x + 1} \right| \ne 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{3}{2}\\x \ne - 1\end{array} \right.\)
Phương trình (1) thành: \(\left| {x + 1} \right|\left( {x - 1} \right) = \left( { - 3x + 1} \right)\left( {2x - 3} \right)\)
TH1: \(x \ge - 1\)
Phương trình thành \({x^2} - 1 = - 6{x^2} + 11x - 3\)\( \Leftrightarrow 7{x^2} - 11x + 2 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{11 + \sqrt {65} }}{{14}}\;\;\left( n \right)\\x = \dfrac{{11 - \sqrt {65} }}{{14}}\;\;\left( n \right)\end{array} \right.\)
TH2: \(x < - 1\)
Phương trình thành \( - {x^2} + 1 = - 6{x^2} + 11x - 3\)\( \Leftrightarrow 5{x^2} - 11x + 4 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{11 + \sqrt {41} }}{{10}}\;\;\left( l \right)\\x = \dfrac{{11 - \sqrt {41} }}{{10}}\;\;\left( l \right)\end{array} \right.\)
Vậy \(S = \left\{ {\dfrac{{11 + \sqrt {65} }}{{14}};\dfrac{{11 - \sqrt {65} }}{{14}}} \right\}\).
Tập nghiệm của phương trình $\dfrac{{{x^2} - 4x - 2}}{{\sqrt {x - 2} }} = \sqrt {x - 2} $ là:
Điều kiện: \(x > 2\)
Ta có$\dfrac{{{x^2} - 4x - 2}}{{\sqrt {x - 2} }} = \sqrt {x - 2} $$ \Leftrightarrow {x^2} - 4x - 2 = x - 2$$ \Leftrightarrow {x^2} - 5x = 0$$ \Leftrightarrow \left[ \begin{array}{l}x = 0\;\;\left( l \right)\\x = 5\;\;\left( n \right)\end{array} \right.$
Vậy \(S = \left\{ 5 \right\}\).
Cho $\dfrac{{{x^2} - 2\left( {m + 1} \right)x + 6m - 2}}{{\sqrt {x - 2} }} = \sqrt {x - 2} $$\left( 1 \right)$. Với \(m\) là bao nhiêu thì $\left( 1 \right)$ có nghiệm duy nhất
Điều kiện $x - 2 > 0 \Leftrightarrow x > 2$.
$\left( 1 \right) \Leftrightarrow {x^2} - \left( {2m + 3} \right)x + 6m = 0$$\left( 2 \right)$, phương trình luôn có nghiệm là $x = 3$ và $x = 2m$
Phương trình $\left( 1 \right)$ có duy nhất \(1\) nghiệm $ \Leftrightarrow \left[ \begin{array}{l}2m \le 2\\2m = 3\end{array} \right.$$ \Leftrightarrow \left[ \begin{array}{l}m \le 1\\m = \dfrac{3}{2}\end{array} \right.$.
Với giá trị nào của tham số \(a\) thì phương trình: \(\left( {{x^2} - 5x + 4} \right)\sqrt {x - a} = 0\) có hai nghiệm phân biệt
Điều kiện: \(x \ge a\)
Phương trình thành \(\left[ \begin{array}{l}{x^2} - 5x + 4 = 0\\x - a = 0\end{array} \right.\)\( \Leftrightarrow \left[ \begin{array}{l}x = 4\\x = 1\\x = a\end{array} \right.\)
+) Nếu \(a<1\) thì phương trình có ba nghiệm phân biệt \(x=a, x=1, x=4\) nên không thỏa mãn yêu cầu.
+) Nếu \(1\le a <4\) thì do điều kiện \(x\ge a\) nên ta loại nghiệm \(x=1\), do đó phương trình có hai nghiệm phân biệt \(x=a,x=4\) (thỏa mãn)
+) Nếu \(a=4\) thì phương trình có nghiệm duy nhất \(x=a=4\) (không thỏa mãn).
+) Nếu \(a> 4\) thì do điều kiện \(x\ge a\) nên ta loại hai nghiệm \(x=1,x=4\), do đó phương trình có nghiệm duy nhất \(x=a\) (không thỏa mãn)
Vậy phương trình có 2 nghiệm phân biệt \( \Leftrightarrow 1 \le a < 4\).
Phương trình : $\left| {3 - x} \right| + \left| {2x + 4} \right| = 3$, có nghiệm là :
Trường hợp 1: \(x < - 2\)
Phương trình thành \(3 - x - 2x - 4 = 3\)\( \Leftrightarrow 3x = - 4\)\( \Leftrightarrow x = \dfrac{{ - 4}}{3}\;\;\left( l \right)\)
Trường hợp 2: \( - 2 \le x \le 3\)
Phương trình thành \(3 - x + 2x + 4 = 3\)\( \Leftrightarrow x = - 4\;\;\left( l \right)\)
Trường hợp 3: \(x > 3\)
Phương trình thành \(x - 3 + 2x + 4 = 3\)\( \Leftrightarrow 3x = 2\)\( \Leftrightarrow x = \dfrac{2}{3}\;\;\left( l \right)\)
Vậy \(S = \emptyset \).
Tổng các nghiệm của phương trình \(4x\left( {x - 1} \right) = \left| {2x - 1} \right| + 1\) bằng:
Phương trình tương đương với \(4{x^2} - 4x - \left| {2x - 1} \right| - 1 = 0\).
Đặt \(t = \left| {2x - 1} \right|,\,\,t \ge 0\). Suy ra \({t^2} = 4{x^2} - 4x + 1 \Rightarrow 4{x^2} - 4x = {t^2} - 1\).
Phương trình trở thành \({t^2} - 1 - t - 1 = 0\)\( \Leftrightarrow {t^2} - t - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}t = - 1\left( {KTM} \right)\\t = 2\left( {TM} \right)\end{array} \right.\)
Với \(t = 2\), ta có \(\left| {2x - 1} \right| = 2 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{2x - 1 = 2}\\{2x - 1 = - 2}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = \dfrac{3}{2}}\\{x = - \dfrac{1}{2}}\end{array}} \right. \Rightarrow \dfrac{3}{2} + \left( { - \dfrac{1}{2}} \right) = 1\)
Tập nghiệm $T$ của phương trình:\(\dfrac{{\left| {x - 3} \right|}}{{\sqrt {x - 4} }} = \dfrac{{x - 3}}{{\sqrt {x - 4} }}\)là:
Điều kiện: \(x > 4\)
Phương trình trở thành:
\(\left| {x - 3} \right| = x - 3\)\( \Leftrightarrow \left\{ \begin{array}{l}x - 3 \ge 0\\\left[ \begin{array}{l}x - 3 = x - 3\\x - 3 = 3 - x\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 3\\\left[ \begin{array}{l}0x = 0\\x = 3\end{array} \right.\end{array} \right.\)\( \Leftrightarrow x \ge 3\)
Vậy \(T = \left( {4; + \infty } \right)\)
Phương trình: \(\left| x \right| + 1 = {x^2} + m\)có 1 nghiệm duy nhất khi và chỉ khi :
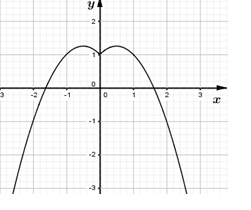
\(\left| x \right| + 1 = {x^2} + m\)\( \Leftrightarrow m = \)\(f\left( x \right) = \left\{ \begin{array}{l} - {x^2} + x + 1\;\;khi\;\;x \ge 0\\ - {x^2} - x + 1\;\;khi\;\;x < 0\end{array} \right.\).
Biểu diễn đồ thị hàm số \(f\left( x \right)\) lên hệ trục tọa độ như hình vẽ bên trên:
+ Vẽ đồ thị hàm số \(y = - {x^2} + x + 1\)
+ Giữ nguyên nhánh đồ thị bên phải trục tung và lấy đối xứng nó qua trục tung.
+ Xóa bỏ phần bên trái trục tung trước đó đi.
Dựa vào đồ thị ta suy ra không tồn tại $m$ để phương trình \(m = f\left( x \right)\) có duy nhất $1$ nghiệm.
Phương trình: \(\left| {x + 2} \right| + \left| {3x - 5} \right| - \left| {2x - 7} \right| = 0\), có nghiệm là:
Trường hợp 1: \(x \le - 2\)
Phương trình thành: \( - x - 2 - 3x + 5 + 2x - 7 = 0\)\( \Leftrightarrow - 2x = 4\)\( \Leftrightarrow x = - 2\;\;\left( n \right)\).
Trường hợp 2: \( - 2 < x < \dfrac{5}{3}\)
Phương trình thành: \(x + 2 - 3x + 5 + 2x - 7 = 0\)\( \Leftrightarrow 0x = 0\;\;\left( {ld} \right)\)
Suy ra \( - 2 < x < \dfrac{5}{3}\).
Trường hợp 3: \(\dfrac{5}{3} \le x \le \dfrac{7}{2}\)
Phương trình thành: \(x + 2 + 3x - 5 + 2x - 7 = 0\)\( \Leftrightarrow 6x = 10\)\( \Leftrightarrow x = \dfrac{5}{3}\;\;\left( n \right)\).
Trường hợp 4: \(x > \dfrac{7}{2}\)
Phương trình thành: \(x + 2 + 3x - 5 - 2x + 7 = 0\)\( \Leftrightarrow 2x = - 4\)\( \Leftrightarrow x = -2 \left( l \right)\)
Vậy \(S = \left[ { - 2;\dfrac{5}{3}} \right]\)
Phương trình\(\left| {\dfrac{{{x^2}}}{2} - 2x + \dfrac{3}{2}} \right| + \left| {\dfrac{{{x^2}}}{2} - 3x + 4} \right| = \dfrac{3}{4}\)có nghiệm là :
Ta có: \(\dfrac{{{x^2}}}{2} - 2x + \dfrac{3}{2} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 3\end{array} \right.;\) \(\dfrac{{{x^2}}}{2} - 3x + 4 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 4\end{array} \right.\)
Từ đó ta phá dấu giá trị tuyệt đối của mỗi biểu thức như sau:
TH1: \(x \le 1\)
Phương trình thành: \(\dfrac{{{x^2}}}{2} - 2x + \dfrac{3}{2} + \dfrac{{{x^2}}}{2} - 3x + 4 = \dfrac{3}{4}\)\( \Leftrightarrow {x^2} - 5x + \dfrac{{19}}{4} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{5 + \sqrt 6 }}{2}\;\;\left( l \right)\\x = \dfrac{{5 - \sqrt 6 }}{2}\;\;\left( l \right)\end{array} \right.\)
TH 2: \(1 < x < 2\)
Phương trình thành: \( - \dfrac{{{x^2}}}{2} + 2x - \dfrac{3}{2} + \dfrac{{{x^2}}}{2} - 3x + 4 = \dfrac{3}{4}\)\( \Leftrightarrow x = \dfrac{7}{4}\;\;\left( n \right)\).
TH 3: \(2 \le x \le 3\)
Phương trình thành: \( - \dfrac{{{x^2}}}{2} + 2x - \dfrac{3}{2} - \dfrac{{{x^2}}}{2} + 3x - 4 = \dfrac{3}{4}\)\( \Leftrightarrow - {x^2} + 5x - \dfrac{{25}}{4} = 0\)\( \Leftrightarrow x = \dfrac{5}{2}\;\;\left( n \right)\)
TH 4: \(3 < x < 4\)
Phương trình thành: \(\dfrac{{{x^2}}}{2} - 2x + \dfrac{3}{2} - \dfrac{{{x^2}}}{2} + 3x - 4 = \dfrac{3}{4}\)\( \Leftrightarrow x = \dfrac{{13}}{4}\;\;\left( n \right)\)
TH 4: \(x \ge 4\)
Phương trình thành: \(\dfrac{{{x^2}}}{2} - 2x + \dfrac{3}{2} + \dfrac{{{x^2}}}{2} - 3x + 4 = \dfrac{3}{4}\)\( \Leftrightarrow {x^2} - 5x + \dfrac{{19}}{4} = 0\)\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{{5 + \sqrt 6 }}{2}\;\;\left( l \right)\\x = \dfrac{{5 - \sqrt 6 }}{2}\;\;\left( l \right)\end{array} \right.\)
Giải phương trình: \(\left| {5x - 1} \right| = 2\).
\(\begin{array}{l}\,\,\,\,\,\left| {5x - 1} \right| = 2\\ \Leftrightarrow 25{x^2} - 10x + 1 = 4\\ \Leftrightarrow 25{x^2} - 10x - 3 = 0\\ \Leftrightarrow \left( {5x - 3} \right)\left( {5x + 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}5x - 3 = 0\\5x + 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{3}{5}\\x = - \dfrac{1}{5}\end{array} \right.\end{array}\)
Vậy \(S = \left\{ {\dfrac{3}{5};\dfrac{{ - 1}}{5}} \right\}\)

