Phương trình: \(\left| x \right| + 1 = {x^2} + m\)có 1 nghiệm duy nhất khi và chỉ khi :
Trả lời bởi giáo viên
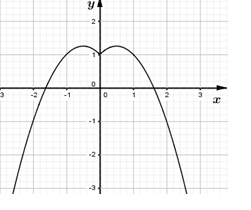
\(\left| x \right| + 1 = {x^2} + m\)\( \Leftrightarrow m = \)\(f\left( x \right) = \left\{ \begin{array}{l} - {x^2} + x + 1\;\;khi\;\;x \ge 0\\ - {x^2} - x + 1\;\;khi\;\;x < 0\end{array} \right.\).
Biểu diễn đồ thị hàm số \(f\left( x \right)\) lên hệ trục tọa độ như hình vẽ bên trên:
+ Vẽ đồ thị hàm số \(y = - {x^2} + x + 1\)
+ Giữ nguyên nhánh đồ thị bên phải trục tung và lấy đối xứng nó qua trục tung.
+ Xóa bỏ phần bên trái trục tung trước đó đi.
Dựa vào đồ thị ta suy ra không tồn tại $m$ để phương trình \(m = f\left( x \right)\) có duy nhất $1$ nghiệm.
Hướng dẫn giải:
- Cô lập \(m\) về dạng \(m = f\left( x \right)\) và phá dấu giá trị tuyệt đối đưa \(f\left( x \right)\) và dạng khoảng.
- Vẽ đồ thị hàm số \(y = f\left( x \right)\) và nhận xét số nghiệm của phương trình chính là số giao điểm của đường thẳng với đồ thị hàm số.

