Cho hình vuông ABCD có cạnh bằng a. Tích \(\overrightarrow {AB} .\overrightarrow {AC} \) bằng:
Vì ABCD là hình vuông cạnh a nên AB = BC = a và AC là phân giác của góc BAD.
\( \Rightarrow \angle BAC = {45^0} = \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\).
Áp dụng định lí Pytago trong tam giác vuông ABC ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2}\\A{C^2} = {a^2} + {a^2} = 2{a^2}\\ \Rightarrow AC = a\sqrt 2 \end{array}\)
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} ;\overrightarrow {AC} } \right)\) \( = a.a\sqrt 2 .\cos {45^0}\)\( = {a^2}\sqrt 2 .\dfrac{{\sqrt 2 }}{2}\) \( = {a^2}\).
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khác \(\overrightarrow 0 \). Xác định góc \(\alpha \) giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\)
Ta có \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.cos\left( {\overrightarrow a ,\overrightarrow b } \right)\).
Mà theo giả thiết \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\), suy ra \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - 1\) \( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = {180^0}\)
Cho tam giác đều \(ABC\) có cạnh bằng \(a\) và chiều cao \(AH\). Mệnh đề nào sau đây là sai?
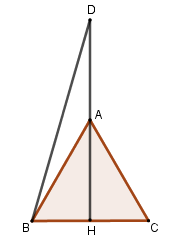
Đáp án A: đúng do \(AH \bot BC\).
Đáp án B: đúng do \(\left( {\overrightarrow {AB} ,\overrightarrow {AH} } \right) = {30^0}\) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {HA} } \right) = {150^0}.\)
Đáp án C: đúng do \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\) \( = a.a.\cos {60^0} = \dfrac{{{a^2}}}{2}\).
Đáp án D: Do \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)\) là góc ngoài của góc \(\widehat C\) nên \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = {120^0}.\)
Do đó \(\overrightarrow {AC} .\overrightarrow {CB} = AC.CB.cos\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)\)\( = a.a.cos{120^0} = - \dfrac{{{a^2}}}{2}\)
Gọi \(G\) là trọng tâm tam giác đều \(ABC\) có cạnh bằng \(a\). Mệnh đề nào sau đây là sai?
Dựa vào đáp án, ta có nhận xét sau:
\( \bullet \) Xác định được góc \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\) là góc \(\widehat A\) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = {60^0}.\)
Do đó \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.cos\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)\( = a.a.cos{60^0} = \dfrac{{{a^2}}}{2}\) . A đúng.
\( \bullet \) Xác định được góc \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)\) là góc ngoài của góc \(\widehat C\) nên \(\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = {120^0}.\)
Do đó \(\overrightarrow {AC} .\overrightarrow {CB} = AC.CB.cos\left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right)\)\( = a.a.cos{120^0} = - \dfrac{{{a^2}}}{2}\) . B đúng.
\( \bullet \) Xác định được góc \(\left( {\overrightarrow {GA} ,\overrightarrow {GB} } \right)\) là góc \(\widehat {AGB}\) nên \(\left( {\overrightarrow {GA} ,\overrightarrow {GB} } \right) = {120^0}.\)
Do đó \(\overrightarrow {GA} .\overrightarrow {GB} = GA.GB.cos\left( {\overrightarrow {GA} ,\overrightarrow {GB} } \right)\)\( = \dfrac{a}{{\sqrt 3 }}.\dfrac{a}{{\sqrt 3 }}.cos{120^0} = - \dfrac{{{a^2}}}{6}\) . C sai.
\( \bullet \) Xác định được góc \(\left( {\overrightarrow {AB} ,\overrightarrow {AG} } \right)\) là góc \(\widehat {GAB}\) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {AG} } \right) = {30^0}.\)
Do đó \(\overrightarrow {AB} .\overrightarrow {AG} = AB.AG.cos\left( {\overrightarrow {AB} ,\overrightarrow {AG} } \right)\)\( = a.\dfrac{a}{{\sqrt 3 }}.cos{30^0} = \dfrac{{{a^2}}}{2}\). D đúng.
Cho tam giác \(ABC\) vuông tại \(A\) và có \(AB = c,{\rm{ }}AC = b.\) Tính \(\overrightarrow {BA} .\overrightarrow {BC} .\)
Ta có \(\overrightarrow {BA} .\overrightarrow {BC} = BA.BC.cos\left( {\overrightarrow {BA} ,\overrightarrow {BC} } \right)\) \( = BA.BC.cos\widehat B = c.\sqrt {{b^2} + {c^2}} .\dfrac{c}{{\sqrt {{b^2} + {c^2}} }} = {c^2}\)
Cách khác. Tam giác \(ABC\) vuông tại \(A\) suy ra \(AB \bot AC\)\( \Rightarrow \,\,\overrightarrow {AB} .\overrightarrow {AC} = 0.\)
Ta có \(\overrightarrow {BA} .\overrightarrow {BC} = \overrightarrow {BA} .\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\) \( = {\overrightarrow {BA} ^2} + \overrightarrow {BA} .\overrightarrow {AC} = A{B^2} = {c^2}\)
Cho hình vuông \(ABCD\) cạnh \(a\). Gọi \(E\) là điểm đối xứng của \(D\) qua \(C.\) Tính \(\overrightarrow {AE} .\overrightarrow {AB} .\)
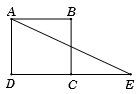
Ta có \(C\) là trung điểm của \(DE\) nên \(DE = 2a.\)
Khi đó \(\overrightarrow {AE} .\overrightarrow {AB} = \left( {\overrightarrow {AD} + \overrightarrow {DE} } \right).\overrightarrow {AB} = \underbrace {\overrightarrow {AD} .\overrightarrow {AB} }_0 + \overrightarrow {DE} .\overrightarrow {AB} \)
\( = DE.AB.\cos \left( {\overrightarrow {DE} ,\overrightarrow {AB} } \right) = DE.AB.\cos {0^0} = 2{a^2}.\)
Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {BC} + \overrightarrow {BD} + \overrightarrow {BA} } \right).\)
Ta có: \(\overrightarrow {BC} + \overrightarrow {BD} + \overrightarrow {BA} \) \( = \left( {\overrightarrow {BC} + \overrightarrow {BA} } \right) + \overrightarrow {BD} = \overrightarrow {BD} + \overrightarrow {BD} = 2\overrightarrow {BD} \) và \(BD = a\sqrt 2 \).
Khi đó \(P = \left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).2\overrightarrow {BD} \)\( = 2\overrightarrow {AB} .\overrightarrow {BD} + 2\overrightarrow {AC} .\overrightarrow {BD} \) \( = - 2\overrightarrow {BA} .\overrightarrow {BD} + 0\)
\( = - 2.BA.BD\cos \left( {\overrightarrow {BA} ,\overrightarrow {BD} } \right)\) \( = - 2.a.a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = - 2{a^2}\)
Cho hình thoi \(ABCD\) có \(AC = 8\) và \(BD = 6.\) Tính \(\overrightarrow {AB} .\overrightarrow {AC} .\)
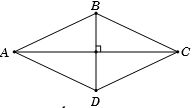
Gọi \(O = AC \cap BD\), giả thiết không cho góc, ta phân tích các vectơ \(\overrightarrow {AB} ,{\rm{ }}\overrightarrow {AC} \) theo các vectơ có giá vuông góc với nhau.Ta có \(\overrightarrow {AB} .\overrightarrow {AC} = \left( {\overrightarrow {AO} + \overrightarrow {OB} } \right).\overrightarrow {AC} = \overrightarrow {AO} .\overrightarrow {AC} + \overrightarrow {OB} .\overrightarrow {AC} \)\( = \dfrac{1}{2}\overrightarrow {AC} .\overrightarrow {AC} + 0 = \dfrac{1}{2}A{C^2} = 32\)
Cho hình chữ nhật \(ABCD\) có \(AB = a\) và \(AD = a\sqrt 2 \). Gọi \(K\) là trung điểm của cạnh \(AD.\) Tính \(\overrightarrow {BK} .\overrightarrow {AC} .\)
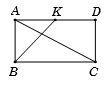
Ta có \(AC = BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 .\)
Ta có \(\left\{ \begin{array}{l}\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \dfrac{1}{2}\overrightarrow {AD} \\\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \end{array} \right.\)
\( \Rightarrow \overrightarrow {BK} .\overrightarrow {AC} = \left( {\overrightarrow {BA} + \dfrac{1}{2}\overrightarrow {AD} } \right)\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\)
\( = \overrightarrow {BA} .\overrightarrow {AB} + \overrightarrow {BA} .\overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {AD} .\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {AD} .\overrightarrow {AD} \) \( = - {a^2} + 0 + 0 + \dfrac{1}{2}{\left( {a\sqrt 2 } \right)^2} = 0\)
Cho tam giác \(ABC\) có \(BC = a,\,{\rm{ }}CA = b,{\rm{ }}AB = c.\) Gọi \(M\) là trung điểm cạnh \(BC.\) Tính \(\overrightarrow {AM} .\overrightarrow {BC} .\)
Vì \(M\) là trung điểm của \(BC\) suy ra \(\overrightarrow {AB} + \overrightarrow {AC} = 2\,\overrightarrow {AM} .\)
Khi đó \(\overrightarrow {AM} .\overrightarrow {BC} = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\overrightarrow {BC} \) \( = \dfrac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right).\left( {\overrightarrow {BA} + \overrightarrow {AC} } \right)\)
\( = \dfrac{1}{2}\left( {\overrightarrow {AC} + \overrightarrow {AB} } \right).\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{1}{2}\left( {{{\overrightarrow {AC} }^2} - {{\overrightarrow {AB} }^2}} \right)\) \( = \dfrac{1}{2}\left( {A{C^2} - A{B^2}} \right) = \dfrac{{{b^2} - {c^2}}}{2}\)
Cho hình vuông \(ABCD\) cạnh \(a\). Tính \(P = \overrightarrow {AC} .\left( {\overrightarrow {CD} + \overrightarrow {CA} } \right).\)
Từ giả thiết suy ra \(AC = a\sqrt 2 .\)
Ta có \(P = \overrightarrow {AC} .\left( {\overrightarrow {CD} + \overrightarrow {CA} } \right) = \overrightarrow {AC} .\overrightarrow {CD} + \overrightarrow {AC} .\overrightarrow {CA} = - \overrightarrow {CA} .\overrightarrow {CD} - {\overrightarrow {AC} ^2}\)
\( = - CA.CD\cos \left( {\overrightarrow {CA} ,\overrightarrow {CD} } \right) - A{C^2} = - a\sqrt 2 .a.\cos {45^0} - {\left( {a\sqrt 2 } \right)^2} = - 3{a^2}.\)
Cho hình vuông \(ABCD\) cạnh \(a.\) Tính \(\overrightarrow {AB} .\overrightarrow {AC} .\)
Ta có \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC} = {45^0}\) nên \(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos {45^0} = a.a\sqrt 2 .\dfrac{{\sqrt 2 }}{2} = {a^2}.\)
Cho tam giác \(ABC\) vuông cân tại \(A\) và có \(AB = AC = a.\) Tính \(\overrightarrow {AB} .\overrightarrow {BC} .\)
Xác định được góc \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\) là góc ngoài của góc \(\widehat B\) nên \(\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right) = {135^0}.\)
Do đó \(\overrightarrow {AB} .\overrightarrow {BC} = AB.BC.cos\left( {\overrightarrow {AB} ,\overrightarrow {BC} } \right)\) \( = a.a\sqrt{2}.cos{135^0} = - a^2\)
Tìm tập các hợp điểm \(M\) thỏa mãn \(\overrightarrow {MB} \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\) với \(A,{\rm{ }}B,{\rm{ }}C\) là ba đỉnh của tam giác.
Gọi \(G\) là trọng tâm tam giác \(ABC\)\( \Rightarrow \overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Ta có \(\overrightarrow {MB} \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right) = 0\) \( \Leftrightarrow \overrightarrow {MB} .3\overrightarrow {MG} = 0 \Leftrightarrow \overrightarrow {MB} .\overrightarrow {MG} = 0\) \( \Leftrightarrow MB \bot MG\) \(\left( * \right)\)
Biểu thức \(\left( * \right)\) chứng tỏ \(MB \bot MG\) hay \(M\) nhìn đoạn \(BG\) dưới một góc vuông nên tập hợp các điểm \(M\) là đường tròn đường kính \(BG.\)
Cho hình thoi ABCD có \(\angle BAD = {60^0}\) và BA = a. Gọi M, N lần lượt là trung điểm của AD, DC. Tính \(\overrightarrow {BM} .\overrightarrow {BN} \) bằng:
Ta có: ABCD là hình thoi có \(\angle BAD = {60^0}\)\( \Rightarrow \angle ABC = {120^0}\) và tam giác ABD là tam giác đều.
\( \Rightarrow AB = AD = BD = a.\)
Áp dụng quy tắc hình bình hành ta có: \(\left\{ \begin{array}{l}\overrightarrow {BM} = \dfrac{1}{2}\left( {\overrightarrow {BA} + \overrightarrow {BD} } \right)\\\overrightarrow {BN} = \dfrac{1}{2}\left( {\overrightarrow {BD} + \overrightarrow {BC} } \right)\end{array} \right..\)
\(\begin{array}{l} \Rightarrow \overrightarrow {BM} .\overrightarrow {BN} = \dfrac{1}{4}\left( {\overrightarrow {BA} + \overrightarrow {BD} } \right)\left( {\overrightarrow {BD} + \overrightarrow {BC} } \right)\\ = \dfrac{1}{4}\left( {\overrightarrow {BA} .\overrightarrow {BD} + \overrightarrow {BA} .\overrightarrow {BC} + {{\overrightarrow {BD} }^2} + \overrightarrow {BD} .\overrightarrow {BC} } \right)\\ = \dfrac{1}{4}\left( {BA.BD.\cos ABD + BA.BC.\cos ABC + B{D^2} + BD.BC.\cos DBC} \right)\\ = \dfrac{1}{4}\left( {{a^2}.\cos {{60}^0} + {a^2}.\cos {{120}^0} + {a^2} + {a^2}.\cos {{60}^0}} \right)\\ = \dfrac{1}{4}\left( {\dfrac{{{a^2}}}{2} - \dfrac{{{a^2}}}{2} + {a^2} + \dfrac{{{a^2}}}{2}} \right) = \dfrac{{3{a^2}}}{8}.\end{array}\)
Cho \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \). Trong các kết quả sau đây, hãy chọn kết quả đúng:
Vì \(\overrightarrow a \) và \(\overrightarrow b \) là hai vectơ cùng hướng và đều khác vectơ \(\overrightarrow 0 \) suy ra \(\left( {\overrightarrow a ,\overrightarrow b } \right) = {0^0}\)
Do đó \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos {0^{\rm{o}}} = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\) nên chọn A.
Cho \(M\) là trung điểm \(AB\), tìm biểu thức sai:
Phương án A:$\overrightarrow {MA} ,\overrightarrow {AB} $ ngược hướng suy ra $\overrightarrow {MA} .\overrightarrow {AB} = MA.AB.\cos {180^{\rm{o}}} = - MA.AB$ nên loại A.
Phương án B:$\overrightarrow {MA} ,\overrightarrow {MB} $ ngược hướng suy ra $\overrightarrow {MA} .\overrightarrow {MB} = MA.MB.\cos {180^{\rm{o}}} = - MA.MB$ nên loại B.
Phương án C: $\overrightarrow {AM} ,\overrightarrow {AB} $ cùng hướng suy ra $\overrightarrow {AM} .\overrightarrow {AB} = AM.AB.\cos {0^{\rm{o}}} = AM.AB$ nên loại C.
Phương án D:$\overrightarrow {MA} ,\overrightarrow {MB} $ ngược hướng suy ra $\overrightarrow {MA} .\overrightarrow {MB} = MA.MB.\;\cos {180^{\rm{o}}} = - MA.MB$ nên chọn D.
Biết \(\overrightarrow a \), \(\overrightarrow b \)\( \ne \overrightarrow 0 \) và \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\). Câu nào sau đây đúng
Ta có \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| \) \(\Leftrightarrow \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| \) \(\Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = - 1\) nên \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng.
Cho tam giác \(ABC\) có cạnh \(BC = 6\) và đường cao \(AH\left( {H \in BC} \right)\) sao cho \(BH = 2HC\). Tính \(\overrightarrow {AB} .\overrightarrow {BC} \)
Ta có:
\(\overrightarrow {AB} .\overrightarrow {BC} = \left( {\overrightarrow {AH} + \overrightarrow {HB} } \right).\overrightarrow {BC} \)\( = \overrightarrow {AH} .\overrightarrow {BC} + \overrightarrow {HB} .\overrightarrow {BC} \) \( = \overrightarrow {HB} .\overrightarrow {BC} = HB.BC.\cos \left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right)\) \( = \dfrac{2}{3}BC.BC.\cos \left( {\overrightarrow {HB} ,\overrightarrow {BC} } \right)\) \( = \dfrac{2}{3}.6.6.\cos {180^0} = - 24\)
Cho tam giác đều \(ABC\) cạnh \(a = 2\). Hỏi mệnh đề nào sau đây sai?
Ta đi tính tích vô hướng ở các phương án. So sánh vế trái với vế phải.
Phương án A:\(\overrightarrow {AB} .\overrightarrow {AC} = AB.AC\cos {60^{\rm{o}}} = 2 \Rightarrow \left( {\overrightarrow {AB} .\overrightarrow {AC} } \right)\overrightarrow {BC} = 2\overrightarrow {BC} \) nên loại A.
Phương án B:\(\overrightarrow {BC} .\overrightarrow {CA} = BC.AC\cos {120^{\rm{o}}} = - 2\) nên loại B.
Phương án C:\(\left( {\overrightarrow {AB} + \overrightarrow {BC} } \right).\overrightarrow {AC} = \overrightarrow {AC} .\overrightarrow {AC} = 4\) nên chọn C.
Phương án D: $\left( {\overrightarrow {BC} - \overrightarrow {AC} } \right).\overrightarrow {BA} = \left( { - \overrightarrow {CB} + \overrightarrow {CA} } \right).\overrightarrow {BA} = \left( {\overrightarrow {CA} - \overrightarrow {CB} } \right).\overrightarrow {BA} = \overrightarrow {BA} .\overrightarrow {BA} = B{A^2} = 4$ nên loại D.

