Câu hỏi:
2 năm trước
Cho hình vuông \(ABCD\) cạnh \(a\). Gọi \(E\) là điểm đối xứng của \(D\) qua \(C.\) Tính \(\overrightarrow {AE} .\overrightarrow {AB} .\)
Trả lời bởi giáo viên
Đáp án đúng: a
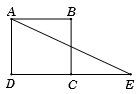
Ta có \(C\) là trung điểm của \(DE\) nên \(DE = 2a.\)
Khi đó \(\overrightarrow {AE} .\overrightarrow {AB} = \left( {\overrightarrow {AD} + \overrightarrow {DE} } \right).\overrightarrow {AB} = \underbrace {\overrightarrow {AD} .\overrightarrow {AB} }_0 + \overrightarrow {DE} .\overrightarrow {AB} \)
\( = DE.AB.\cos \left( {\overrightarrow {DE} ,\overrightarrow {AB} } \right) = DE.AB.\cos {0^0} = 2{a^2}.\)
Hướng dẫn giải:
Xen điểm thích hợp và tính tích vô hướng của các véc tơ.

