Câu hỏi:
2 năm trước
Cho hình chữ nhật \(ABCD\) có \(AB = a\) và \(AD = a\sqrt 2 \). Gọi \(K\) là trung điểm của cạnh \(AD.\) Tính \(\overrightarrow {BK} .\overrightarrow {AC} .\)
Trả lời bởi giáo viên
Đáp án đúng: a
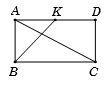
Ta có \(AC = BD = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 .\)
Ta có \(\left\{ \begin{array}{l}\overrightarrow {BK} = \overrightarrow {BA} + \overrightarrow {AK} = \overrightarrow {BA} + \dfrac{1}{2}\overrightarrow {AD} \\\overrightarrow {AC} = \overrightarrow {AB} + \overrightarrow {AD} \end{array} \right.\)
\( \Rightarrow \overrightarrow {BK} .\overrightarrow {AC} = \left( {\overrightarrow {BA} + \dfrac{1}{2}\overrightarrow {AD} } \right)\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)\)
\( = \overrightarrow {BA} .\overrightarrow {AB} + \overrightarrow {BA} .\overrightarrow {AD} + \dfrac{1}{2}\overrightarrow {AD} .\overrightarrow {AB} + \dfrac{1}{2}\overrightarrow {AD} .\overrightarrow {AD} \) \( = - {a^2} + 0 + 0 + \dfrac{1}{2}{\left( {a\sqrt 2 } \right)^2} = 0\)
Hướng dẫn giải:
Biểu diễn các véc tơ \(\overrightarrow {BK} \) và \(\overrightarrow {AC} \) qua các véc tơ \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \) rồi thực hiện nhân vô hướng véc tơ
Câu hỏi khác
- Bài tập giá trị lượng giác của một góc bất kì từ 0 đến 180 độ toán 10 có lời giải
- Bài tập hệ thức lượng trong tam giác toán 10 có lời giải
- Bài tập tích vô hướng của hai véc tơ toán 10 có lời giải
- Bài tập biểu thức tọa độ của tích vô hướng toán 10 có lời giải
- Bài tập tổng hợp câu hay và khó chương tích vô hướng của hai véc tơ toán 10 có lời giải
