Bất đẳng thức

Ta có:

\(f\left( x \right) = \dfrac{{\left( {x + 2} \right)\left( {x + 8} \right)}}{x}\)\( = \dfrac{{{x^2} + 8x + 2x + 16}}{x}\)\( = \dfrac{{{x^2} + 10x + 16}}{x}\)\( = x + \dfrac{{16}}{x} + 10\)

Áp dụng bất đẳng thức Cô-si cho hai số dương \(x\) và \(\dfrac{{16}}{x}\) ta có:

\(\begin{array}{l}x + \dfrac{{16}}{x} \ge 2\sqrt {x.\dfrac{{16}}{x}} \Leftrightarrow x + \dfrac{{16}}{x} \ge 8\end{array}\)

\( \Rightarrow x + \dfrac{{16}}{x} + 10 \ge 8 + 10\)\( \Rightarrow x + \dfrac{{16}}{x} + 10 \ge 18\)

\( \Rightarrow f\left( x \right) \ge 18\)

Dấu “\( = \)” xảy ra \(\left\{ \begin{array}{l}x > 0\\x = \dfrac{{16}}{x}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x > 0\\x^2 = 16\end{array} \right.\)\( \Leftrightarrow x = 4\).

\(\min f\left( x \right) = 18 \Leftrightarrow x = 4\)

Vậy \(m = 18\)

Thay \(m = 18\)  vào biểu thức \({m^2} + 1\) ta có: \({18^2} + 1 = 325\)

Điều kiện: \(\left\{ \begin{array}{l}x \ge 0\\x + 2 \ge 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ge  - 2\end{array} \right.\)\( \Leftrightarrow x \ge 0\)

Ta có: \(5\sqrt x  \ge 0\) với mọi \(x \in R\)

\(x\sqrt {x + 2}  \ge 0\) với mọi \(x \in R\)

\( \Rightarrow 5\sqrt x  + x\sqrt {x + 2}  \ge 0\) với mọi \(x \in R\)

\( \Rightarrow  - 8 + 5\sqrt x  + x\sqrt {x + 2}  \ge  - 8\) với mọi \(x \in R\)

\( \Rightarrow A \ge  - 8\) với mọi \(x \in R\)

Dấu “\( = \)” xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}5\sqrt x  = 0\\x\sqrt {x + 2}  = 0\end{array} \right.\)\( \Leftrightarrow x = 0\)

Vậy \(\min A =  - 8 \Leftrightarrow x = 0\)

Vì $x^2\ge 0$ nên $1-x^2\le 1$, ngoài ra $\sqrt{1-x^2}\ge 0,\forall x\in [-1;1]$.

Do đó: \(f\left( x \right) \ge 0\) và \(f\left( 1 \right) = 0\); \(f\left( x \right) \le 1\) và \(f\left( 0 \right) = 1\).

Vậy hàm số \(f\left( x \right)\) có giá trị nhỏ nhất bằng \(0\) và giá trị lớn nhất bằng \(1\).

Gọi \(a,b\) lần lượt là hai kích thước của hình chữ nhật có chu vi không đổi \(C\), khi đó \(a + b = \dfrac{C}{2}\).

Áp dụng bất đẳng thức Cô – si cho hai số dương \(a,b\) ta có:

\(a + b \ge 2\sqrt {ab}  \Leftrightarrow ab \le {\left( {\dfrac{{a + b}}{2}} \right)^2} = \dfrac{{{C^2}}}{4} = const\)

Dấu “=” xảy ra khi và chỉ khi \(a = b\).

Vậy trong các hình chữ nhật có cùng chu vi thì hình vuông là hình có diện tích lớn nhất.

Đáp án A: sai trong trường hợp nếu \(c < 0\) thì bất đẳng thức bị đổi chiều.

Đáp án B: sai trong trường hợp \(a < 0 < b\).

Đáp án C: sai chẳng hạn \( - 3 < 1\) và \( - 4 < 1\) nhưng \(\left( { - 3} \right).\left( { - 4} \right) > 1.1\).

Đáp án D: đúng theo tính chất nhân cả hai vế của bất đẳng thức với cùng một số dương thì bất đẳng thức không đổi chiều.

Đáp án A sai chẳng hạn \( - 1 >  - 2\) và \( - 1 >  - 3\) nhưng \(\left( { - 1} \right).\left( { - 1} \right) < \left( { - 2} \right).\left( { - 3} \right)\).

Đáp án B sai vì \( - 1 >  - 3\) và \( - 1 >  - 2\) nhưng \(\dfrac{{ - 1}}{{ - 1}} < \dfrac{{ - 3}}{{ - 2}}\).

Đáp án C sai vì \(1 > 0\) và \(1 >  - 1\) nhưng \(1 - 1 < 0 - \left( { - 1} \right)\).

Đáp án D đúng theo tính chất nhân từng vế BĐT khi các vế đều dương.

Ta có: \(P =  - a + \sqrt a  =  - {\left( {\sqrt a } \right)^2} + \sqrt a  = \dfrac{1}{4} - {\left( {\sqrt a  - \dfrac{1}{2}} \right)^2} \le \dfrac{1}{4}\)

Vậy GTLN của $P$ là \(\dfrac{1}{4}\) đạt được tại $a=\dfrac{1}{4}$.

Ta sẽ chứng minh \(P\) không có GTNN.

Đặt \(\sqrt a  = t \ge 0\) thì \(P =  - {t^2} + t\)

Xét hàm số bậc hai \(y = f\left( t \right) =  - {t^2} + t\) trên \(\left[ {0; + \infty } \right)\) ta có \(t =  - \dfrac{b}{{2a}} = \dfrac{1}{2}\)

Bảng biến thiên:

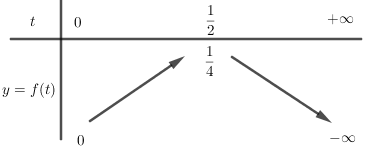
Từ bảng biến thiên ta thấy hàm số không đạt GTNN hay không tồn tại GTNN của \(P\).

Kết luận: \(P\) đạt GTLN bằng \(\dfrac{1}{4}\) tại \(a = \dfrac{1}{4}\) và không có GTNN.

Ta có: \({x^2} - 5x + 9 = {\left( {x - \dfrac{5}{2}} \right)^2} + \dfrac{{11}}{4} \ge \dfrac{{11}}{4};\forall x \in \mathbb{R}\)

Suy ra: \(f\left( x \right) = \dfrac{2}{{{x^2} - 5x + 9}} \le \dfrac{8}{{11}}\)

Vậy giá trị lớn nhất của hàm số bằng \(\dfrac{8}{{11}}\)

Dấu \( = \) xảy ra khi \(x - \dfrac{5}{2} = 0 \Leftrightarrow x = \dfrac{5}{2}\)

Áp dụng bất đẳng thức Cô – si cho hai số không âm \(x\), \(y\). Ta có: \(\sqrt {xy}  \le \dfrac{{x + y}}{2} = 6\).

Ta có: \(\dfrac{a}{b} + \dfrac{b}{a} \ge 2\sqrt {\dfrac{a}{b}.\dfrac{b}{a}}  = 2 \Rightarrow \left( I \right)\) đúng;

\(\dfrac{a}{b} + \dfrac{b}{c} + \dfrac{c}{a} \ge 3\sqrt[3]{{\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{a}}} = 3 \Rightarrow \left( {II} \right)\)đúng;

$\left. \begin{array}{l}a + b \ge 2\sqrt {ab} \\\dfrac{1}{a} + \dfrac{1}{b} \ge 2\sqrt {\dfrac{1}{{ab}}} \end{array} \right\}$$ \Rightarrow \left( {a + b} \right)\left( {\dfrac{1}{a} + \dfrac{1}{b}} \right) \ge 4$$ \Rightarrow (III)$ đúng.

Ta có:

\(x - y = \left( {a + b} \right)\left( {c + d} \right) - \left( {a + c} \right)\left( {b + d} \right)\)\( = ac + bc + ad + bd - ab - cb - ad - cd\) \( = ac + bd - ab - cd \) \(= a\left( {c - b} \right) - d\left( {c - b} \right)\) \( = \left( {a-d} \right)\left( {c-b} \right) < 0\) do \(a < b < c < d\)

Suy ra: \(x < y\).

\(x - z = \left( {a + b} \right)\left( {c + d} \right) - \left( {a + d} \right)\left( {b + c} \right)\) \( = ac + ad + bc + bd - ab - ac - bd - cd\) \( = ad + bc - ab - cd\) \( = a\left( {d - b} \right) - c\left( {d - b} \right)\) \( = \left( {a - c} \right)\left( {d - b} \right) < 0\) do \(a < b < c < d\)

Suy ra \(x < z\)

\(y - z = \left( {a + c} \right)\left( {b + d} \right) - \left( {a + d} \right)\left( {b + c} \right)\) \( = ab + bc + ad + cd - ab - bd - ac - cd\) \( = bc + ad - bd - ac \) \(= b\left( {c - d} \right) - a\left( {c - d} \right)\) \( = \left( {b - a} \right)\left( {c - d} \right) < 0\) do \(a < b < c < d\)

Suy ra \(y < z\)

Vậy \(x < y < z\)

Ta có: \(f\left( x \right) = \dfrac{x}{2} + \dfrac{2}{{x - 1}} = \dfrac{{x - 1}}{2} + \dfrac{2}{{x - 1}} + \dfrac{1}{2} \ge 2\sqrt {\dfrac{{x - 1}}{2}.\dfrac{2}{{x - 1}}}  + \dfrac{1}{2} = \dfrac{5}{2}\)

Vậy hàm số \(f\left( x \right)\) có giá trị nhỏ nhất bằng \(\dfrac{5}{2}\)

Dấu \( = \) xảy ra khi \(\dfrac{{x - 1}}{2} = \dfrac{2}{{x - 1}} \Leftrightarrow x = 3\)

Ta có \(f\left( x \right) \ge 0\) và \({\left[ {f\left( x \right)} \right]^2} = \dfrac{{x - 2}}{{{x^2}}} = \dfrac{1}{x} - \dfrac{2}{{{x^2}}} =-2\left(\dfrac{1}{x^2}-\dfrac{1}{2x}\right)\\=-2\left(\dfrac{1}{x^2}-2.\dfrac{1}{x}.\dfrac{1}{4}+\dfrac{1}{4^2}\right)+2.\dfrac{1}{4^2}\\= \dfrac{1}{8} - 2{\left( {\dfrac{1}{x} - \dfrac{1}{4}} \right)^2} \le \dfrac{1}{8} \Rightarrow 0 \le f\left( x \right) \le \dfrac{1}{{2\sqrt 2 }}\)

Vậy giá trị lớn nhất của hàm số bằng \(\dfrac{1}{{2\sqrt 2 }}\)

Dấu \( = \) xảy ra khi \(\dfrac{1}{x} = \dfrac{1}{4} \Leftrightarrow x = 4\)

Ta có:

\(\begin{array}{l}P + 3 = \dfrac{a}{{b + c}} + 1 + \dfrac{b}{{c + a}} + 1 + \dfrac{c}{{a + b}} + 1\\ = \dfrac{{a + b + c}}{{b + c}} + \dfrac{{a + b + c}}{{c + a}} + \dfrac{{a + b + c}}{{a + b}}\\ = \left( {a + b + c} \right)\left( {\dfrac{1}{{b + c}} + \dfrac{1}{{c + a}} + \dfrac{1}{{a + b}}} \right)\end{array}\)

Áp dụng bất đẳng thức \(\dfrac{1}{x} + \dfrac{1}{y} + \dfrac{1}{z} \ge \dfrac{9}{{x + y + z}}\) suy ra: \(\dfrac{1}{{b + c}} + \dfrac{1}{{c + a}} + \dfrac{1}{{a + b}} \ge \dfrac{9}{{2\left( {a + b + c} \right)}}\).

$=>P + 3 \ge (a+b+c).\dfrac{9}{{2\left( {a + b + c} \right)}}$

Do đó \(P + 3 \ge \dfrac{9}{2} \Rightarrow P \ge \dfrac{3}{2}\); đẳng thức xảy ra khi \(a = b = c\).

Hàm số xác định khi \(\left\{ \begin{array}{l}x + 3 \ge 0\\6 - x \ge 0\end{array} \right. \Leftrightarrow  - 3 \le x \le 6\) nên TXĐ \({\rm{D}} = \left[ { - 3;6} \right].\)

Ta có \({f^2}\left( x \right) = 9 + 2\sqrt {\left( {x + 3} \right)\left( {6 - x} \right)} \).

\( \bullet \) Vì $\sqrt {\left( {3 + x} \right)\left( {6 - x} \right)}  \ge 0,\,\,\forall x \in \left[ { - \,3;6} \right]$ nên suy ra \({f^2}\left( x \right) \geqslant 9 \Rightarrow f\left( x \right) \geqslant 3.\)

Dấu \('' = ''\) xảy ra \( \Leftrightarrow x =  - 3\) hoặc \(x = 6.\) Vậy $m = 3.$

\( \bullet \) Lại có $2\sqrt {\left( {3 + x} \right)\left( {6 - x} \right)}  \le 3 + x + 6 - x = 9$ nên suy ra \({f^2}\left( x \right) \leqslant 18 \Rightarrow f\left( x \right) \leqslant 3\sqrt 2 .\)

Dấu \('' = ''\) xảy ra \( \Leftrightarrow x + 3 = 6 - x \Leftrightarrow x = \dfrac{3}{2}.\) Vậy $M = 3\sqrt 2 .$

Vậy $m = 3,\,\,\,M = 3\sqrt 2 .$

Hàm số xác định khi \(\left\{ \begin{array}{l}x - 4 \ge 0\\8 - x \ge 0\end{array} \right. \Leftrightarrow 4 \le x \le 8\) nên TXĐ \({\rm{D}} = \left[ {4;8} \right].\)

- Ta có \({f^2}\left( x \right) = 3x - 8 + 4\sqrt {\left( {x - 4} \right)\left( {8 - x} \right)}  = 3\left( {x - 4} \right) + 4\sqrt {\left( {x - 4} \right)\left( {8 - x} \right)}  + 4.\)

Vì $\left\{ \begin{array}{l}x - 4 \ge 0\\\sqrt {\left( {x - 4} \right)\left( {8 - x} \right)}  \ge 0\end{array} \right.,\,\,\forall x \in \left[ {4;8} \right]$ nên suy ra \({f^2}\left( x \right) \geqslant 4 \Rightarrow f\left( x \right) \geqslant 2.\)

Dấu \('' = ''\) xảy ra \( \Leftrightarrow x = 4.\)

Vậy $m = 2.$

- Lại có, áp dụng bất đẳng thức Bunhia – Copxki cho bộ các số \(\left( {2;1} \right),\left( {\sqrt {x - 4} ;\sqrt {8 - x} } \right)\) ta có :

 \(f\left( x \right) = 2\sqrt {x - 4}  + 1.\sqrt {8 - x}  \le \sqrt {\left( {{2^2} + {1^2}} \right)\left[ {{{\left( {\sqrt {x - 4} } \right)}^2} + {{\left( {\sqrt {8 - x} } \right)}^2}} \right]}  = \sqrt {5.4}  = 2\sqrt 5 \)

Dấu  xảy ra $ \Leftrightarrow \dfrac{2}{{\sqrt {x - 4} }} = \dfrac{1}{{\sqrt {8 - x} }} \Leftrightarrow x = \dfrac{{36}}{5}$

Vậy $M = 2\sqrt 5 .$

Vậy $m = 2,\,\,\,M = 2\sqrt 5 .$

Từ giả thiết, ta có $3\left( {x + y} \right) - 4 = {x^2} + {y^2} \ge \dfrac{{{{\left( {x + y} \right)}^2}}}{2}$

$ \Leftrightarrow {\left( {x + y} \right)^2} - 6\left( {x + y} \right) + 8 \le 0$

Đặt \(x + y = t\) ta được \({t^2} - 6t + 8 \le 0\) \( \Leftrightarrow \left( {t - 2} \right)\left( {t - 4} \right) \le 0\) \( \Leftrightarrow 2 \le t \le 4\)

Do đó $2 \le x + y \le 4$

Ta có \(\dfrac{1}{x} + \dfrac{4}{y} = 1.\left( {\dfrac{1}{x} + \dfrac{4}{y}} \right) = \left( {x + y} \right)\left( {\dfrac{1}{x} + \dfrac{4}{y}} \right) = 5 + \dfrac{{4x}}{y} + \dfrac{y}{x} \ge 5 + 2\sqrt {\dfrac{{4x}}{y}.\dfrac{y}{x}}  = 9.\)

Dấu \('' = ''\) xảy ra khi

\(\dfrac{{4x}}{y} = \dfrac{y}{x}\) và \(x + y = 1\) hay \(x = \dfrac{1}{3};{\rm{ }}y = \dfrac{2}{3}\).

Ta có: \(\dfrac{1}{x} = a + \dfrac{1}{{a + 1}}\) và \(\dfrac{1}{y} = b + \dfrac{1}{{b + 1}}\).

Suy ra: \(\dfrac{1}{x} - \dfrac{1}{y} = \left( {a - b} \right)\left[ {1 - \dfrac{1}{{\left( {a + 1} \right)\left( {b + 1} \right)}}} \right]\)

Do \(a > b > 0\) nên \(a + 1 > 1\) và \(b + 1 > 1\) suy ra: \(\dfrac{1}{{\left( {a + 1} \right)\left( {b + 1} \right)}} < 1\)\( \Rightarrow 1 - \dfrac{1}{{\left( {a + 1} \right)\left( {b + 1} \right)}} > 0\).

Vậy \(\dfrac{1}{x} - \dfrac{1}{y} > 0\)\( \Leftrightarrow \dfrac{1}{x} > \dfrac{1}{y}\) do \(x > 0\) và \(y > 0\) nên \(\dfrac{1}{x} > \dfrac{1}{y} \Leftrightarrow x < y\).

Ta có:

\(\begin{array}{l}{\left( {m + n} \right)^2} \ge 4mn\\ \Leftrightarrow {m^2} + 2mn + {n^2} \ge 4mn\\ \Leftrightarrow {m^2} + {n^2} \ge 2mn\end{array}\)