Bất đẳng thức

$\left\{ \begin{array}{l}a > b > 0\\c > d > 0\end{array} \right. \Rightarrow ac > bd$ đúng theo tính chất nhân hai bất đẳng thức dương cùng chiều.

$a > b > 0$\( \Leftrightarrow \)$a + 1 > b + 1 > 1$\( \Leftrightarrow \)$\dfrac{a}{{a + 1}} > \dfrac{b}{{b + 1}}$.

Điều kiện: 

\(\left\{ \begin{array}{l}x - 2 \ge 0\\4 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \le 4\end{array} \right. \Leftrightarrow 2 \le x \le 4\)

\(A = \sqrt {x - 2}  + \sqrt {4 - x} \) có tập xác định \(D = \left[ {2;\,4} \right]\).

Ta có: \({A^2}=(\sqrt {x - 2}  + \sqrt {4 - x})^2\)

\(=x-2+4-x+2\sqrt {\left( {x - 2} \right)\left( {4 - x} \right)}  \)

\(= 2 + 2\sqrt {\left( {x - 2} \right)\left( {4 - x} \right)}  \ge 2 \)

(Do $\sqrt {\left( {x - 2} \right)\left( {4 - x} \right)} \ge 0 \forall 2 \le x \le 4$)

\(\Rightarrow A \ge \sqrt 2 \), dấu bằng xảy ra khi $\sqrt {\left( {x - 2} \right)\left( {4 - x} \right)} = 0$

\( \Leftrightarrow \left[ \begin{array}{l}x - 2 = 0\\4 - x = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 4\end{array} \right.\)

$\Leftrightarrow$ \(x = 2\) hoặc \(x = 4\).

Ta có: \(P = {x^2} + \dfrac{{16}}{x}\)\( = {x^2} + \dfrac{8}{x} + \dfrac{8}{x}\)\(\mathop  \ge \limits^{Cosi} 3\sqrt[3]{{{x^2}.\dfrac{8}{x}.\dfrac{8}{x}}} = 12\).

Vậy \({P_{\min }} = 12\).

Theo bất đẳng thức Côsi ta có \(2x + \dfrac{3}{x} \ge 2\sqrt 6 \) suy ra giá trị nhỏ nhất của \(f\left( x \right)\) bằng \(2\sqrt 6 \).

Ta có \(P = 7\left( {{x^4} + {y^4}} \right) + 4{x^2}{y^2}\)

\( = 7\left[ {\left( {{x^2} + {y^2}} \right) - 2{x^2}{y^2}} \right] + 4{x^2}{y^2}\)

\( = 7\left( {{x^2} + {y^2}} \right) - 10{x^2}{y^2}\)

\( = \dfrac{7}{4}{\left[ {2\left( {{x^2} + {y^2}} \right)} \right]^2} - 10{x^2}{y^2}\)

\( = \dfrac{7}{4}{\left( {1 + xy} \right)^2} - 10{x^2}{y^2} = \dfrac{7}{4} + \dfrac{7}{2}xy - \dfrac{{33}}{4}{\left( {xy} \right)^2}\)

Theo giả thiết, \(2\left( {{x^2} + {y^2}} \right) = 1 + xy \Rightarrow 2\left[ {{{\left( {x + y} \right)}^2} - 2xy} \right] = 1 + xy\)

\( \Rightarrow 5xy + 1 = 2{\left( {x + y} \right)^2} \ge 0 \Rightarrow xy \ge  - \dfrac{1}{5}\,\,\left( * \right)\)

Lại có \(2\left( {{x^2} + {y^2}} \right) \ge 4xy \Rightarrow 1 + xy \ge 4xy \Rightarrow xy \le \dfrac{1}{3}\,\,\left( {**} \right)\)

Từ \(\left( * \right)\) và \(\left( {**} \right)\) suy ra \(xy \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).

Đặt \(t = xy\), suy ra \(t \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).

Khi đó \(P =  - \dfrac{{33}}{4}{t^2} + \dfrac{7}{2}t + \dfrac{7}{4}\) với \(t \in \left[ { - \dfrac{1}{5};\dfrac{1}{3}} \right]\).

Ta có bảng biến thiên:

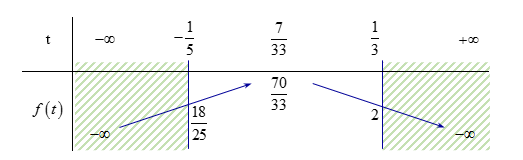
Dựa vào bảng biến thiên, suy ra GTLN của \(P\) là \(M = \dfrac{{70}}{{33}}\) và GTNN của \(P\) là \(m = \dfrac{{18}}{{25}}\).

Vậy \(M + m = \dfrac{{18}}{{25}} + \dfrac{{70}}{{33}} = \dfrac{{2344}}{{825}}\).

Với mọi \(a\), \(b\), \(c\) dương ta luôn có:

\(\dfrac{a}{b} + \dfrac{b}{a} \ge 2\sqrt {\dfrac{a}{b}.\dfrac{b}{a}}  \Leftrightarrow \dfrac{a}{b} + \dfrac{b}{a} \ge 2\), dấu bằng xảy ra khi \(a = b\). Vậy \(\left( I \right)\) đúng.

\(\dfrac{a}{b} + \dfrac{b}{c} + \dfrac{c}{a} \ge 3\sqrt[3]{{\dfrac{a}{b}.\dfrac{b}{c}.\dfrac{c}{a}}} \Leftrightarrow \dfrac{a}{b} + \dfrac{b}{c} + \dfrac{c}{a} \ge 3\), dấu bằng xảy ra khi \(a = b = c\). Vậy \(\left( {II} \right)\) đúng.

\(\left( {a + b + c} \right).\left( {\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}} \right) \ge 3\sqrt[3]{{abc}}.3\sqrt[3]{{\dfrac{1}{{abc}}}} = 9\)\( \Rightarrow \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{9}{{a + b + c}}\), dấu bằng xảy ra khi \(a = b = c\). Vậy \(\left( {III} \right)\) đúng.

Vậy \(\left( I \right)\), \(\left( {II} \right)\), \(\left( {III} \right)\) đúng.

Ta có \(F = \dfrac{{{x^2} + {y^2}}}{{x - y}} = \dfrac{{{x^2} - 2xy + {y^2} + 2xy}}{{x - y}} = \dfrac{{{{\left( {x - y} \right)}^2} + 2.1000}}{{x - y}} = x - y + \dfrac{{2.1000}}{{x - y}}.\)

Áp dụng bất đẳng thức Côsi, ta có \(F = x - y + \dfrac{{2.1000}}{{x - y}} \ge 2\sqrt {\left( {x - y} \right).\dfrac{{2.1000}}{{x - y}}}  = 40\sqrt 5 .\)

Dấu  xảy ra $ \Leftrightarrow \left\{ \begin{array}{l}xy = 1000\\x - y = \dfrac{{2.1000}}{{x - y}} > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}xy = 1000\\x - y = 20\sqrt 5 \end{array} \right..$

Vậy ${F_{\min }} = 40\sqrt 5 $ khi $\left\{ \begin{array}{l}ab = 1000\\a - b = 20\sqrt 5 \end{array} \right. $

$\Rightarrow {a^2} + {b^2} = {\left( {a - b} \right)^2} + 2ab =(20\sqrt 5)^2+2.1000= 4000 $

$\Rightarrow \dfrac{{{a^2} + {b^2}}}{{1000}} = 4.$

\(x - 1 + \dfrac{1}{{x - 1}} \ge 2\), \(\forall x \in \left( {1;\, + \infty } \right)\)\( \Leftrightarrow x + \dfrac{1}{{x - 1}} \ge 3\), \(\forall x \in \left( {1;\, + \infty } \right)\).

Dấu  xảy ra khi \(x - 1 = \dfrac{1}{{x - 1}}\)\( \Leftrightarrow {x^2} - 2x = 0\)\( \Leftrightarrow x = 2\), \(\forall x \in \left( {1;\, + \infty } \right)\).

Vậy \(m = \mathop {\min y}\limits_{\left( {1; + \infty } \right)}  = 3\).

Xét hàm số \(y = \dfrac{{4{x^4} - 3{x^2} + 9}}{{{x^2}}}\)\( = 4{x^2} + \dfrac{9}{{{x^2}}} - 3\).

Áp dụng bất đẳng thức Cô si, ta có \(4{x^2} + \dfrac{9}{{{x^2}}}\) \( \ge 2\sqrt {4{x^2}.\dfrac{9}{{{x^2}}}} \)\( = 12\)\( \Rightarrow \)\(y \ge 9\).

Vậy giá trị nhỏ nhất của hàm số \(y = \dfrac{{4{x^4} - 3{x^2} + 9}}{{{x^2}}}\) là \(9\) khi \(4{x^2} = \dfrac{9}{{{x^2}}}\)\( \Leftrightarrow {x^2} = \dfrac{3}{2}\)\( \Leftrightarrow x =  \pm \dfrac{{\sqrt 6 }}{2}\).

Đặt cạnh của hình chữ nhật lần lượt là \(x\), \(y\)(\(x\), \(y > 0\); \(y\) là cạnh của bức tường).

Ta có: \(2x + y = 100\).\(\left( 1 \right)\).

Diện tích hình chữ nhật là \(S = xy = 2.x.\dfrac{y}{2}\mathop  \le \limits^{Cosi} 2.{\left( {\dfrac{{x + \dfrac{y}{2}}}{2}} \right)^2} = \dfrac{1}{8}{\left( {2x + y} \right)^2} = \dfrac{1}{8}{\left( {100} \right)^2} = 1250\).

Vậy \({S_{\max }} = 1250\,{{\rm{m}}^{\rm{2}}}\). Đạt được khi \(x = \dfrac{y}{2} \Leftrightarrow y = 2x \Rightarrow x = 25\,{\rm{m}}\); \(y = 50\,{\rm{m}}\).

Áp dụng bất đẳng thức Cô - si, ta có

\({x^2} + \dfrac{y}{{zx}} + \dfrac{z}{{xy}} \ge 3.\sqrt[3]{{{x^2}.\dfrac{y}{{zx}}.\dfrac{z}{{xy}}}} = 3;\)\({y^2} + \dfrac{x}{{yz}} + \dfrac{z}{{xy}} \ge 3;\) \({z^2} + \dfrac{x}{{yz}} + \dfrac{y}{{zx}} \ge 3\)

Cộng từng vế của ba bất đẳng thức trên, ta được ${x^2} + {y^2} + {z^2} + 2\left( {\dfrac{x}{{yz}} + \dfrac{y}{{zx}} + \dfrac{z}{{xy}}} \right) \ge 9$.

Suy ra \(P \ge \dfrac{9}{2}\). Khi $x = y = z = 1$ thì \(P = \dfrac{9}{2}.\)

Ta có ${f^2}\left( x \right) = {\left( {x + \sqrt {8 - {x^2}} } \right)^2}$$ = {x^2} + 2x\sqrt {8 - {x^2}}  + 8 - {x^2}$ $ = 8 + 2x\sqrt {8 - {x^2}} $

Áp dụng bất đẳng thức Côsi, ta có $2x\sqrt {8 - {x^2}}  \le {x^2} + {\left( {\sqrt {8 - {x^2}} } \right)^2} = 8$

$ \Rightarrow {f^2}\left( x \right) = 8 + 2x\sqrt {8 - {x^2}}  \le 8 + 8 = 16$$ \Rightarrow f\left( x \right) \le 4$

Dấu \('' = ''\) xảy ra $ \Leftrightarrow \left\{ \begin{array}{l}{x^2} = {\left( {\sqrt {8 - {x^2}} } \right)^2}\\2x\sqrt {8 - {x^2}}  = 8\end{array} \right. \Leftrightarrow x = 2.$

Vậy $M = 4.$

      Hàm số xác định khi \(\left\{ \begin{array}{l}7 - 2x \ge 0\\3x + 4 \ge 0\end{array} \right. \Leftrightarrow  - \dfrac{4}{3} \le x \le \dfrac{7}{2}\) nên TXĐ \({\rm{D}} = \left[ { - \dfrac{4}{3};\dfrac{7}{2}} \right].\)

Ta có ${y^2} = {\left( {\sqrt {7 - 2x}  + \sqrt {3x + 4} } \right)^2} = 7 - 2x + 2\sqrt {\left( {7 - 2x} \right)\left( {3x + 4} \right)}  + 3x + 4$

$ = x + 11 + 2\sqrt {\left( {7 - 2x} \right)\left( {3x + 4} \right)}  = \dfrac{1}{3}\left( {3x + 4} \right) + 2\sqrt {\left( {7 - 2x} \right)\left( {3x + 4} \right)}  + \dfrac{{29}}{3}.$

Vì $\left\{ \begin{array}{l}3x + 4 \ge 0\\\sqrt {\left( {7 - 2x} \right)\left( {3x + 4} \right)}  \ge 0\end{array} \right.,\,\,\forall x \in \left[ { - \dfrac{4}{3};\dfrac{7}{2}} \right]$ nên suy ra

Dấu \('' = ''\) xảy ra \( \Leftrightarrow x =  - \dfrac{4}{3}.\) Vậy $m = \dfrac{{\sqrt {87} }}{3}.$

Theo BĐT CAUCHY – SCHAWARS: $\dfrac{{{a_1}^2}}{{{b_1}}} + \dfrac{{{a_2}^2}}{{{b_2}}} + ... + \dfrac{{{a_n}^2}}{{{b_n}}} \ge \dfrac{{{{({a_1} + {a_2} + ... + {a_n})}^2}}}{{{b_1} + {b_2} + ... + {b_n}}}$, trong đó các số ${b_i} > 0$

Vì \(0 < x < 1\) nên \(x > 0\) và \(1 - x > 0\)

Từ đó \(y = \dfrac{4}{x} + \dfrac{9}{{1 - x}}\)\( = \dfrac{{{2^2}}}{x} + \dfrac{{{3^2}}}{{1 - x}}\)\( \ge \dfrac{{{{\left( {2 + 3} \right)}^2}}}{{x + 1 - x}} = 25\)

Suy ra \({y_{\min }} = 25\) khi \(x = \dfrac{2}{5}\)\( = \dfrac{a}{b}\)\( \Rightarrow a + b = 7\).

Ta có: \(x + y + xy \ge 7\)\( \Leftrightarrow x\left( {1 + y} \right) \ge 7 - y\) \( \Leftrightarrow x \ge \dfrac{{7 - y}}{{1 + y}}\) (vì \(y > 0 \Rightarrow 1 + y > 0\))

Do đó \(S = x + 2y\)\( \ge \dfrac{{7 - y}}{{1 + y}} + 2y = 2y - 1 + \dfrac{8}{{y + 1}}\) \( = 2\left( {y + 1} \right) + \dfrac{8}{{y + 1}} - 3\).

Áp dụng bất đẳng thức Cô – si cho hai số không âm \(2\left( {y + 1} \right)\) và \(\dfrac{8}{{y + 1}}\) ta có:

\(2\left( {y + 1} \right) + \dfrac{8}{{y + 1}} - 3 \ge 2\sqrt {2\left( {y + 1} \right).\dfrac{8}{{y + 1}}}  - 3 = 5\) hay \(S \ge 5\).

Dấu bằng xảy ra khi \(\left\{ \begin{array}{l}2\left( {y + 1} \right) = \dfrac{8}{{y + 1}}\\x = \dfrac{{7 - y}}{{1 + y}}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 3\end{array} \right.\).

Vậy \({S_{\min }} = 5\) khi \(x = 3,y = 1\).

Từ giả thiết, ta có \(xy\left( {x + y} \right) = x + y + 3xy\). \(\left( * \right)\)

Vì \(x > 0,{\rm{ }}y > 0\) nên \(x + y > 0\). Do đó $\left( * \right) \Leftrightarrow x + y = \dfrac{1}{x} + \dfrac{1}{y} + 3 \ge \dfrac{4}{{x + y}} + 3$

$ \Leftrightarrow {\left( {x + y} \right)^2} - 3\left( {x + y} \right) - 4 \ge 0 \Leftrightarrow \left[ \begin{array}{l}x + y \le  - 1\\x + y \ge 4\end{array} \right. \Leftrightarrow x + y \ge 4$ (do \(x,y > 0\)).

Áp dụng bất đẳng thức Côsi cho hai số thực dương, ta có

$\dfrac{x}{2} + \dfrac{1}{{2x}} \ge 2\sqrt {\dfrac{x}{2}.\dfrac{1}{{2x}}}  = 2.\dfrac{1}{{\sqrt 4 }} = 1$ và $\dfrac{y}{2} + \dfrac{2}{y} \ge 2\sqrt {\dfrac{y}{2}.\dfrac{2}{y}}  = 2.$

Khi đó $F = x + y + \dfrac{1}{{2x}} + \dfrac{2}{y} = \dfrac{{x + y}}{2} + \left( {\dfrac{x}{2} + \dfrac{1}{{2x}}} \right) + \left( {\dfrac{y}{2} + \dfrac{2}{y}} \right) \ge \dfrac{3}{2} + 1 + 2 = 4\dfrac{1}{2}.$

Dấu  xảy ra $ \Leftrightarrow \left\{ \begin{array}{l}x + y = 3\\\dfrac{x}{2} = \dfrac{1}{{2x}};\,\,\dfrac{y}{2} = \dfrac{2}{y}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right..$ Vậy ${F_{\min }} = 4\dfrac{1}{2}.$

Từ giả thiết suy ra ${a^2} + {b^2} + {c^2} \le 4.$

Ta có $4 = {a^2} + {b^2} + {c^2} + abc = {a^2} + {b^2} + {c^2} + \sqrt {{a^2}{b^2}{c^2}} .$

Áp dụng bất đẳng thức Côsi, ta có \(\dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^3}}}{{27}} \ge {a^2}{b^2}{c^2}\).

Từ đó suy ra $4 \le {a^2} + {b^2} + {c^{2}} + \sqrt {\dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^3}}}{{27}}} $

Đặt \(S=a^2+b^2+c^2\) ta được:

$\begin{array}{l}
\sqrt {\frac{{{S^3}}}{{27}}} \ge 4 - S \Leftrightarrow \frac{{{S^3}}}{{27}} \ge 16 - 8S + {S^2}\\
\Leftrightarrow {S^3} \ge 432 - 216S + 27{S^2}\\
\Leftrightarrow {S^3} - 27{S^2} + 216S - 432 \ge 0\\
\Leftrightarrow \left( {S - 3} \right)\left( {{S^2} - 24S + 144} \right) \ge 0\\
\Leftrightarrow \left( {S - 3} \right){\left( {S - 12} \right)^2} \ge 0\\
\Leftrightarrow S - 3 \ge 0\\
\Leftrightarrow S \ge 3
\end{array}$

Do đó \(3\le S\le 4\).

S=3 khi a=b=c=1, S=4 chẳng hạn tại a=0 và b=c=2.

Vậy GTNN của S bằng 3 và GTLN của S bằng 4.

Áp dụng bất đẳng thức Cô-si cho 2 số không âm a,b ta được:

\(a + b \ge 2\sqrt {ab}  = 2.1 = 2\)

Vậy B đúng