Trong mặt phẳng tọa độ Oxy, cho hai điểm B(−3;6),C(1;−2). Xác định điểm E thuộc đoạn BC sao cho BE=2EC
Vì E thuộc đoạn BC và BE=2EC suy ra →BE=2→EC
Gọi E(x;y) khi đó →BE(x+3;y−6),→EC(1−x;−2−y)
Do đó {x+3=2(1−x)y−6=2(−2−y)⇔{x=−13y=23
Vậy E(−13;23)
Cho →u=(m2+m−2;4) và →v=(m;2). Tìm m để hai vecto →u,→v cùng phương
+ Với m=0: Ta có →u=(−2;4);→v=(0;2)
Vì 0−2≠24 nên hai vectơ →u;→vkhông cùng phương
+ Với m≠0: Ta có →u;→vcùng phương khi và chỉ khi
m2+m−2m=42⇔m2−m−2=0⇔[m=−1m=2
Vậy với m=−1 và m=2 là các giá trị cần tìm.
Cho tam giác ABC có M,N,P lần lượt là trung điểm của BC,CA,AB. Biết M(1;1),N(−2;−3),P(2;−1). Chọn đáp án đúng nhất:
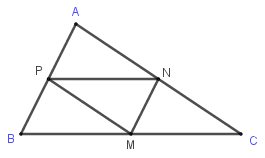
Ta có →MN(−3;−4),→PA(xA−2;yA+1)
→MN=→PA⇔{−3=xA−2−4=yA+1⇔{xA=−1yA=−5⇒A(−1;−5)
N là trung điểm AC suy ra {xN=xA+xC2yN=yA+yC2⇔{−2=−1+xC2−3=−5+yC2⇔{xC=−3yC=−1⇒C(−3;−1)
Tương tự M là trung điểm BCsuy ra B(5;3)
Cho →a=(1;3),→b=(−3;0);→c=(−1;2). Phân tích vectơ →c qua →a;→b
Giả sử →c=x→a+y→b.
Ta có
→a=(1;3),→b=(−3;0)
x.→a+y→b=x.(1;3)+y(−3;0)=(x.1;x.3)+(−3.y;0.y)=(x;3x)+(−3y;0)=(x−3y;3x+0)
=>x→a+y→b=(x−3y;3x)
Suy ra {x−3y=−13x=2⇔{x=23y=59 ⇒→c=23→a+59→b
Cho tam giác ABCcó A(3;4),B(−1;2),C(4;1). A′ là điểm đối xứng của A qua B,B′ là điểm đối xứng của B qua C,C′ là điểm đối xứng của C qua A. Chọn kết luận “không” đúng:
A′ là điểm đối xứng của A qua B suy ra B là trung điểm của AA′
Do đó {xB=xA+xA′2yB=yA+yA′2⇔{−1=3+xA′22=4+yA′2⇔{xA′=−5yA′=0⇒A′(−5;0)
Tương tự B′(9;0),C′(2;7)
Trọng tâm của tam giác ABC và A′B′C′ có cùng tọa độ là (2;73)
Vậy các đáp án B, C, D đều đúng.
Trong mặt phẳng tọa độ Oxy cho A(3;−1),B(−1;2) và I(1;−1). Gọi C,D là các điểm sao cho tứ giác ABCD là hình bình hành, biết I là trọng tâm tam giác ABC. Tìm tọa tâm Ocủa hình bình hành ABCD.
Vì I là trọng tâm tam giác ABC nên
xI=xA+xB+xC3⇒xC=3xI−xA−xB=1
yI=yA+yB+yC3⇒yC=3yI−yA−yB=−4
Suy ra C(1;−4)
Điểm O là tâm của hình bình hành ABCD suy ra O là trung điểm AC do đó
xO=xA+xC2=2,yO=yA+yC2=−52⇒O(2;−52)
Cho tam giác ABC có A(2;1),B(−1;−2),C(−3;2). Xác định trọng tâm tam giác ABC
G là trọng tâm tam giác suy ra
xG=xA+xB+xC3=2−1−33=−23 và yG=yA+yB+yC2=1−2+23=13
Vậy G(−23;13)
Cho ba điểm A(−4;0),B(0;3) và C(2;1). Tìm điểm M sao cho →MA+2→MB+3→MC=→0
Gọi M(x;y), ta có →MA(−4−x;−y),→MB(−x;3−y),→MC(2−x;1−y)
Suy ra →MA+2→MB+3→MC=(−6x+2;−6y+9)
Do đó →MA+2→MB+3→MC=→0⇒{−6x+2=0−6y+9=0⇔{x=13y=32
Vậy M(13;32)
Cho →a=(1;2),→b=(−3;4);→c=(−1;3). Tìm tọa độ của vectơ →u biết 3→u+2→a+3→b=3→c
Ta có 3→u+2→a+3→b=3→c⇔→u=−23→a−→b+→c
Suy ra →u=(−23+3−1;−43−4+3)=(43;−73)
Trong mặt phẳng Oxy, cho 3 vecto: →a=(3;2)→b=(−1;5)→c=(−2;−5). Tìm tọa độ của vectơ→k=2→a+→b và →l=−→a+2→b+5→c
Ta có 2→a=(6;4)→b=(−1;5)suy ra →k=(6−1;4+5)=(5;9);
−→a=(−3;−2),2→b=(−2;10) và 5→c=(−10;−25)suy ra
→l=(−3−2−10;−2+10−25)=(−15;−17)
Cho hình bình hành ABCD có AD=4 và chiều cao ứng với cạnh AD=3, ^BAD=600. Chọn hệ trục tọa độ (A;→i,→j) sao cho →i và →AD cùng hướng, yB>0 . Tìm khẳng định sai?

Kẻ BH⊥AD⇒BH=3;AB=BHsin600=3√3/2=2√3;AH=√AB2−BH2=√12−9=√3,
Do đó:
A(0;0);B(√3;3),C(4+√3;3)D(4;0)→AB=(√3;3),→BC=(4;0),→CD=(−√3;−3)→AC=(4+√3;3)
Trong mặt phẳng tọa độ Oxy. Cho hình thoi ABCD cạnh a và ^BAD=600. Biết A trùng với gốc tọa độ O,C thuộc trục Ox và xB≥0,yB≥0. Tìm tọa độ các đỉnh của hình thoi ABCD

Từ giả thiết ta xác định được hình thoi trên mặt phẳng tọa độ Oxy
Gọi I là tâm hình thoi ta có BI=ABsin^BAI=asin300=a2
AI=√AB2−BI2=√a2−a24=a√32
Suy ra A(0;0),B(a√32;a2),C(a√3;0),D(a√32;−a2)
Trong hệ trục tọa độ Oxy cho hình vuông ABCD tâm I và có A(1;3). Biết điểm B thuộc trục Ox và →BC cùng hướng với →i. Tìm tọa độ các vectơ →AB,→BC
Từ giả thiết ta xác định được hình vuông trên mặt phẳng tọa độ

Vì điểm A(1;3) suy ra AB=3,OB=1
Do đó B(1;0),C(4;0),D(4;3)
Vậy →AB(0;−3),→BC(3;0)
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC,CA,AB, O là điểm bất kì. Khẳng định nào sau đây là đúng nhất?

Theo quy tắc ba điểm ta có
→OA+→OB+→OC=(→OP+→PA)+(→OM+→MB)+(→ON+→NC)=(→OM+→ON+→OP)+→PA+→MB+→NC=(→OM+→ON+→OP)−(→BM+→CN+→AP)
Vì PN,MN là đường trung bình của tam giác ABC nên
PN//BM,MN//BP suy ra tứ giác BMNP là hình bình hành
⇒→BM=→PN
N là trung điểm của AC⇒→CN=→NA
Do đó theo quy tắc ba điểm ta có
→BM+→CN+→AP=(→PN+→NA)+→AP=→PA+→AP=→0
Do đó →OA+→OB+→OC=→OM+→ON+→OP
Cho hình thoi ABCD cạnh a và ^BCD=600. Gọi O là tâm hình thoi. Chọn kết luận đúng:
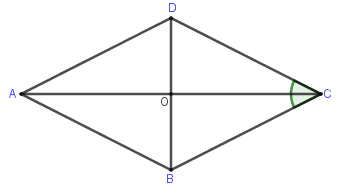
Ta có |→AB+→AD|=|→AC| (quy tắc hình bình hành)
Xét tam giác BCD có CD=CB=a và góc ^BCD=600 nên tam giác BCD đều cạnh a
Xét tam giác DOC có ˆO=900 và DC=a,DO=12DB=a2 nên CO=√DC2−DO2=√a2−a24=a√32
Do đó AC=2OC=2.a√32=a√3 hay |→AB+→AD|=a√3 nên A đúng.
Lại có:
→OB−→DC=→DO−→DC=→CO nên |→OB−→DC|=|→CO|=CO=a√32
|→OB−→DC|=|→CO|=a√32≠a√34 nên B sai.
Cho hình vuông ABCD có tâm là O và cạnh a. M là một điểm bất kỳ. Chứng minh rằng →u=→MA+→MB−→MC−→MD không phụ thuộc vị trí điểm M. Tính độ dài vectơ →u
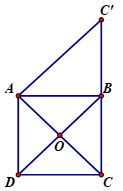
Theo quy tắc phép trừ ta có
→u=(→MA−→MC)+(→MB−→MD)=→CA+→DB
Suy ra →u không phụ thuộc vị trí điểm M.
Qua A kẻ đường thẳng song song với DB cắt BC tại C′.
Khi đó tứ giác ADBC′ là hình bình hành (vì có cặp cạnh đối song song) suy ra →DB=→AC′
Do đó →u=→CA+→AC′=→CC′
=> |→u|=|→CC′|=CC′=BC+BC′
Mà ta có BC′=AD=a (do ADBC′ là hình bình hành) và BC=a (gt)
Vậy |→u|=a+a=2a
Cho tam giác ABC vuông tại A có và BC=a√5. Tính độ dài của vectơ →AB+→AC.

Gọi D là điểm sao cho tứ giác ABDC là hình bình hành.
Khi đó theo quy tắc hình bình hành ta có →AB+→AC=→AD
Vì tam giác ABC vuông ở A nên tứ giác ABDC là hình chữ nhật suy ra AD=BC=a√5
Vậy |→AB+→AC|=|→AD|=AD=a√5
Cho hình bình hành ABCD. Trên các đoạn thẳngDC,AB theo thứ tự lấy các điểm M,N sao cho DM=BN. Gọi P là giao điểm của AM,DB và Q là giao điểm của CN,DB. Khẳng định nào sau đây là đúng?
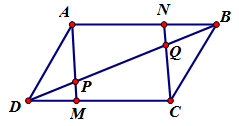
Ta có DM=BN⇒AN=MC, mặt khác AN song song với MC do đó tứ giác ANCM là hình bình hành
Suy ra →AM=→NC.
Xét tam giác ΔDMP và ΔBNQ ta có DM=NB (giả thiết), ^PDM=^QBN (so le trong)
Mặt khác ^DMP=^APB (đối đỉnh) và ^APQ=^NQB (hai góc đồng vị) suy ra ^DMP=^BNQ.
Do đó ΔDMP=ΔBNQ (c.g.c) suy ra DP=QB.
Dễ thấy →DP,→QB cùng hướng vì vậy →DP=→QB.
Cho tam giác ABC có trọng tâm G. Gọi I là trung điểm của BC. Dựng điểm B' sao cho \overrightarrow {B'B} = \overrightarrow {AG} , gọi J là trung điểm của BB'. Khẳng định nào sau đây là đúng?

Ta có \overrightarrow {B'B} = \overrightarrow {AG} suy ra B'B = AG.
Dễ thấy \overrightarrow {BJ} ,\,\,\overrightarrow {IG} cùng hướng (1).
Vì G là trọng tâm tam giác ABC nên IG = \dfrac{1}{2}AG, J là trung điểm BB' suy ra BJ = \dfrac{1}{2}BB'
Vì vậy BJ = IG (2)
Từ (1) và (2) ta có \overrightarrow {BJ} = \overrightarrow {IG} .
Cho tam giác ABC đều cạnh a và G là trọng tâm. Gọi I là trung điểm của AG. Tính độ dài của vectơ \overrightarrow {BI} .

Ta có \left| {\overrightarrow {AB} } \right| = AB = a
Gọi M là trung điểm của BC \Rightarrow BM = \dfrac{1}{2}BC = \dfrac{a}{2}
Tam giác ABM vuông tại M nên AM = \sqrt {A{B^2} - B{M^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 3 }}{2}
Ta có \left| {\overrightarrow {AG} } \right| = AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}
Mà I là trung điểm của AG nên MI = AG = \dfrac{{a\sqrt 3 }}{3}
\left| {\overrightarrow {BI} } \right| = BI = \sqrt {B{M^2} + M{I^2}} = \sqrt {\dfrac{{{a^2}}}{4} + \dfrac{{{a^2}}}{3}} = \dfrac{{a\sqrt {21} }}{6}

