Trong các đẳng thức sau đây, đẳng thức nào đúng ?
Vì α=1500 là góc tù nên sinα>0,cosα<0,tanα=sinαcosα<0,cotα<0.
Do đó các đáp án A, B, D đều sai. Ta chỉ xét đáp án C. Ta có tan150∘=−tan30∘=−1√3.
Cho hình bình hành ABCD. M là điểm bất kì, khi đó:
Đáp án A ta có:
{→MC−→MA=→AC→MB−→MD=→DB→AC≠→DB ⇒→MC−→MA≠→MB−→MD
⇒ đáp án A sai.
Đáp án B ta có:
{→MC−→MA=→AC→DA−→DC=→CA→AC≠→CA ⇒→MC−→MA≠→DA−→DC
⇒ B sai.
Đáp án C ta có:
{→MC−→MA=→AC→AB+→AD=→AC ⇒→MC−→MA=→AB+→AD
⇒ C đúng.
Cho tứ giác ABCD có →AD=→BC. Mệnh đề nào trong các mệnh đề sau là sai?

Dựa vào hình vẽ ta thấy ABCD là hình bình hành nên A đúng.
⇒AD=BC⇒ B đúng.
Hai vectơ →AB và →DC cùng hướng và AB = DC nên →AB=→DC⇒D đúng.
Vậy C sai. (2 đường chéo của hình bình hành không bằng nhau)
Cho ba điểm A, B, C phân biệt. Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng là:
Điều kiện cần và đủ để ba điểm A, B, C thẳng hàng là 2 vectơ →AB và →AC cùng phương
⇔∃k≠0:→AB=k→AC.
Cho tam giác ABC, có BC = a, CA = b, AB = c. Mệnh đề nào sau đây đúng?
Nếu cosA>0 thì góc A nhọn hay b2+c2−a2>0 thì góc A nhọn.
Cho hai vectơ →a=(4;3),→b=(1;7). Góc giữa hai vectơ →a và →b là?
cos(→a;→b)=→a.→b|→a|.|→b| =4.1+3.7√42+32.√12+72=25√25.√50 =√22
Do đó góc giữa hai véc tơ bằng 450.
Cho hai tam giác ABC và A’B’C’ lần lượt có trọng tâm G và G’. Đẳng thức nào dưới đây là sai?
Vì G và G’ lần lượt là trọng tâm của tam giác ABC và A’B’C’ nên ta có:
→GA+→GB+→GC=→0→G′A′+→G′B′+→G′C′=→0.
Với điểm M bất kì khác điểm G ta chứng minh: 3→MG=→MA+→MB+→MC
Ta có: →MA+→MB+→MC =→MG+→GA+→MG+→GB+→MG+→GC=3→MG
Tương tự ta có: 3→MG′=→MA′+→MB′+→MC′
Từ đó suy ra
3→GG′=3(→MG′−→MG)=3→MG′−3→MG=→MA′+→MB′+→MC′−→MA−→MB−→MC=(→MA′−→MA)+(→MB′−→MB)+(→MC′−→MC)=→AA′+→BB′+→CC′.
Nên A đúng.
Đáp án B:
3→GG′=→GG′+→GG′+→GG′=→GA+→AC′+→C′G′+→GB+→BA′+→A′G′+→GC+→CB′+→B′G′=(→GA+→GB+→GC)+(→AC′+→BA′+→CB′)+(→C′G′+→A′G′+→B′G′)=→0+(→AC′+→BA′+→CB′)+→0=→AC′+→BA′+→CB′
Nên B đúng.
Đáp án C:
3→GG′=→GG′+→GG′+→GG′=→GA+→AB′+→B′G′+→GB+→BC′+→C′G′+→GC+→CA′+→A′G′=(→GA+→GB+→GC)+(→AB′+→BC′+→CA′)+(→B′G′+→C′G′+→A′G′)=→0+(→AB′+→BC′+→CA′)+→0=→AB′+→BC′+→CA′
Nên C đúng.
D sai do A đúng.
Tam giác ABC vuông cân tại A có AB = AC = a. Đường trung tuyến BM có độ dài là?
BM2=BA2+BC22−AC24=a2+2a22−a24=5a24⇒BM=a√52.
Trong mặt phẳng Oxy cho ba điểm A(−1;1),B(2;4),C(6;0). Khi đó tam giác ABC là tam giác
Ta có:
→AB=(3;3),→AC=(7;−1),→BC=(4;−4)
Do →AB.→BC=3.4+3.(−4)=0 nên AB⊥BC hay tam giác ABC vuông tại B
Cho tam giác ABC và I thỏa mãn →IA=3→IB. Đẳng thức nào sau đây là đẳng thức đúng.
Ta có:
→CI=→CA−→IA=→CA−3→IB=→CA−3(→CB−→CI)⇔→CI=→CA−3→CB+3→CI⇔2→CI=3→CB−→CA⇔→CI=12(3→CB−→CA)
Cho tam giác ABC đều cạnh bằng 1. Tính →AB.→BC ?
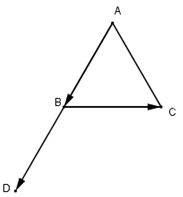
Lấy điểm D sao cho →AB=→BD⇒(→AB,→BC)=(→BD;→BC)=1200
⇒→AB.→BC=|→AB|.|→BC|.cos(→AB,→BC)=1.1.cos1200=−12
(vì tam giác ABC đều cạnh 1 nên AB=BC=1⇒|→AB|=|→BC|=1)
Cho hình thang vuông ABCD có đáy lớn AB=4a, đáy nhỏ CD=2a, đường cao AD=3a; I là trung điểm của AD . Khi đó (→IA+→IB).→ID bằng:

Ta có (→IA+→IB).→ID=(→IA+→IA+→AB).→ID=2→IA.→ID=−9a22 nên chọn B.
Trong mặt phẳngOxy cho A(−1;1), B(1;3), C(1;−1). Khẳng định nào sau đây đúng.
Phương án A: do →AB=(2;2) nên loại A.
Phương án B: →AB=(2;2), →BC=(0;−4), →AB.→BC=−8 suy ra →AB không vuông góc →BC nên loại B.
Phương án C: Ta có →AB=(2;2), →AC=(2;−2), →BC=(0;−4), suy ra AB=AC=√8, →AB.→AC=0.
Nên tam giác ABC vuông cân tại A. Do đó chọn C.
Cho 2 vectơ →a và →bcó độ dài bằng 1 thỏa|→a+→b|=2. Hãy xác định (3→a−4→b)(2→a+5→b)
|→a|=|→b|=1,|→a+→b|=2⇔(→a+→b)2=4⇔→a.→b=1, (3→a−4→b)(2→a+5→b)=6→a2−20→b2+7→a.→b=−7
Cho 2 vectơ →a và →b có |→a|=4, |→b|=5 và (→a,→b)=120o. Tính |→a+→b|
Ta có |→a+→b|=√(→a+→b)2=√→a2+→b2+2→a.→b=√|→a|2+|→b|2+2|→a||→b|cos(→a,→b)=√21
Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 600. Tàu thứ nhất chạy với tốc độ 30km/h, tàu thứ hai chạy với tốc độ 40km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?

Ta có: Sau 2h quãng đường tàu thứ nhất chạy được là: S1=30.2=60km.
Sau 2h quãng đường tàu thứ hai chạy được là: S2=40.2=80km.
Vậy: sau 2h hai tàu cách nhau là: S=√S12+S22−2S1.S2.cos600=20√13.
Cho tam giác ABC biết A(−1;2),B(2;0),C(−3;1). Tìm tọa độ điểm M thuộc BC sao cho SABM=13SABC.

Giả sử M(x; y) là điểm thỏa mãn điều kiện đề bài.
Kẻ AH vuông góc với BC. Suy ra
12BM.AH=13.12AH.BC⇒→BM=13→BC(x−2;y)=13(−5;1)⇔{x−2=−53y=13⇔{x=13y=13⇒M(13;13).
Cho hình vuông ABCD cạnh a, tâm O. Gọi M là điểm tùy ý trên đường tròn nội tiếp hình vuông. Tính \overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MC} .\overrightarrow {MD} .
Ta có
\begin{array}{l}\overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MC} .\overrightarrow {MD} = \left( {\overrightarrow {MO} + \overrightarrow {OA} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)\left( {\overrightarrow {MO} + \overrightarrow {OD} } \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2M{O^2} + \overrightarrow {OA} .\overrightarrow {OB} + \overrightarrow {OC.} \overrightarrow {OD} + \overrightarrow {MO} \left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} } \right).\end{array}
Có \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ;\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0
\overrightarrow {OA} \bot \overrightarrow {OB} \Rightarrow \overrightarrow {OA} .\overrightarrow {OB} = 0,\overrightarrow {OC} \bot \overrightarrow {OD} \Rightarrow \overrightarrow {OC} .\overrightarrow {OD} = 0
Đường tròn nội tiếp hình vuông cạnh a có bán kính \dfrac{a}{2} \Rightarrow MO = \dfrac{a}{2} \Rightarrow M{O^2} = \dfrac{{{a^2}}}{4}.
Vậy \overrightarrow {MA} .\overrightarrow {MB} + \overrightarrow {MC} .\overrightarrow {MD} = 2.\dfrac{{{a^2}}}{4} = \dfrac{{{a^2}}}{2}
Cho ba vector \overrightarrow a ,\,\,\overrightarrow b ,\,\,\overrightarrow c thỏa mãn \left| {\overrightarrow a } \right| = a,\,\,\left| {\overrightarrow b } \right| = b,\,\,\left| {\overrightarrow c } \right| = c và \overrightarrow a + \overrightarrow b + 3\overrightarrow c = \overrightarrow 0 . Tính A = \overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow c + \overrightarrow c .\overrightarrow a
Ta có \overrightarrow a + \overrightarrow b + 3\overrightarrow c = \overrightarrow 0 \Leftrightarrow \overrightarrow a + \overrightarrow b + \overrightarrow c = - 2\overrightarrow c \Leftrightarrow {\left( {\overrightarrow a + \overrightarrow b + \overrightarrow c } \right)^2} = 4{\overrightarrow c ^2} \Leftrightarrow {a^2} + {b^2} + {c^2} + 2A = 4{c^2}
Do đó A = \dfrac{1}{2}\left( {3{c^2} - {a^2} - {b^2}} \right).
Cho tam giác ABC với tọa độ các đỉnh A\left( {1;\,\, - 3} \right),\,\,B\left( {3;\,\, - 5} \right),\,\,C\left( {2;\,\, - 2} \right). Tìm tọa độ giao điểm E của BC với phân giác trong của góc A.
Ta có A{B^2} = 8,\,\,A{C^2} = 2 \Rightarrow \dfrac{{AC}}{{AB}} = \dfrac{1}{2}
Giả sử E (x; y) thuộc đoạn BC. Theo tính chất đường phân giác ta có:
\begin{array}{l}\dfrac{{EB}}{{AB}} = \dfrac{{EC}}{{AC}} \Rightarrow \dfrac{{EC}}{{EB}} = \dfrac{{AC}}{{AB}} = \dfrac{1}{2}.\\ \Rightarrow \dfrac{{\overrightarrow {EC} }}{{\overrightarrow {EB} }} = - \dfrac{1}{2}\\ \Leftrightarrow \left( {2 - x;\,\, - 2 - y} \right) = - \dfrac{1}{2}\left( {3 - x;\,\, - 5 - y} \right)\\ \Leftrightarrow \left\{ \begin{array}{l}2 - x = - \dfrac{3}{2} + \dfrac{1}{2}x\\ - 2 - y = \dfrac{5}{2} + \dfrac{1}{2}y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{3}\\y = - 3\end{array} \right.\\ \Rightarrow E\left( {\dfrac{7}{3}; - 3} \right)\end{array}

