Cho tam giác ABC vuông cân tại A. Tính cos góc giữa hai trung tuyến BE,CF.
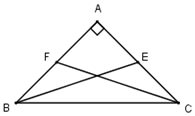
Gọi a là góc tạo bởi hai trung tuyến BE,CF.
Khi đó $\cos a = \dfrac{{\left| {\overrightarrow {BE} .\overrightarrow {CF} } \right|}}{{\left| {\overrightarrow {BE} } \right|\left| {\overrightarrow {CF} } \right|}}$
Sử dụng phân tích
$\begin{array}{l}\overrightarrow {BE} .\overrightarrow {CF} = \left( {\overrightarrow {BA} + \overrightarrow {AE} } \right)\left( {\overrightarrow {CA} + \overrightarrow {AF} } \right)\\ = \overrightarrow {BA} .\overrightarrow {CA} + \overrightarrow {BA} .\overrightarrow {AF} + \overrightarrow {AE} .\overrightarrow {CA} + \overrightarrow {AE} .\overrightarrow {AF} \\ = 0 - \overrightarrow {AB} .\dfrac{{\overrightarrow {AB} }}{2} - \overrightarrow {AC} \dfrac{{\overrightarrow {AC} }}{2} + 0\\ = - \dfrac{{A{B^2}}}{2} - \dfrac{{A{C^2}}}{2} = - \dfrac{{A{B^2}}}{2} - \dfrac{{A{B^2}}}{2} = - A{B^2}.\end{array}$
$BE = CF = \sqrt {A{B^2} + A{E^2}} = \sqrt {A{B^2} + \dfrac{{A{B^2}}}{4}} = AB\sqrt {\dfrac{5}{4}} $
Từ đó suy ra $\cos a = \dfrac{{A{B^2}}}{{A{B^2}\dfrac{5}{4}}} = \dfrac{4}{5}.$
Xác định dạng của tam giác $ABC$ biết rằng $S = \dfrac{{\sqrt 3 }}{{36}}{\left( {a + b + c} \right)^2}$
Theo công thức He-rong ta có
$\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} = \dfrac{{\sqrt 3 }}{9}{p^2} \Leftrightarrow \left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) = \dfrac{1}{{27}}{p^3}$
Theo bất đẳng thức Cauchy ta có $\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right) \le \dfrac{{{{\left( {p - a + p - b + p - c} \right)}^3}}}{{27}} = \dfrac{{{{\left( {3p - \left( {a + b + c} \right)} \right)}^3}}}{{27}} = \dfrac{{{{\left( {3p - 2p} \right)}^3}}}{{27}} = \dfrac{{{p^3}}}{{27}}$
Đẳng thức xảy ra khi a = b = c.
Khi đó tam giác $ABC$ đều.
Cho các số thực $a = {x^2} + x + 1,\,\,b = 2x + 1,\,\,c = {x^2} - 1$. Xác định điều kiện của x để a, b, c là độ dài ba cạnh của một tam giác.
Để a, b, c là độ dài ba cạnh của tam giác khi và chỉ khi $\left\{ \begin{array}{l}a,\,\,b,\,\,c > 0\\a + b > c,\,\,b + c > a,\,\,a + c > b\end{array} \right.$
\(\left\{ \begin{array}{l}{x^2} + x + 1 > 0\,\\2x + 1 > 0\\{x^2} - 1 > 0\\{x^2} + 3x + 2 > {x^2} - 1\\{x^2} + 2x > {x^2} + x + 1\\2{x^2} + x > 2x + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > - \dfrac{1}{2}\\\left[ \begin{array}{l}x > 1\\x < - 1\end{array} \right.\\x > 1\\x > 1\\\left[ \begin{array}{l}x > 1\\x < - \dfrac{1}{2}\end{array} \right.\end{array} \right. \Leftrightarrow x > 1\)
Tìm bán kính đường tròn ngoại tiếp tam giác $ABC $ biết $ b = 7cm,\,\,c = 5 cm,\,\,{\mathop{\rm cosA}\nolimits} = \dfrac{3}{5}$.
Theo định lí cosin ta có ${a^2} = {b^2} + {c^2} - 2bc\cos A = {7^2} + {5^2} - 2.7.5.\dfrac{3}{5} = 32 \Rightarrow a = 4\sqrt 2 $
Từ công thức ${\sin ^2}A + {\cos ^2}A = 1 \Rightarrow {\mathop{\rm sinA}\nolimits} = \dfrac{4}{5}$
Theo định lí sin ta có $\dfrac{a}{{\sin A}} = 2R \Rightarrow R = \dfrac{a}{{2\sin A}} = \dfrac{{4\sqrt 2 }}{{2.\dfrac{4}{5}}} = \dfrac{{5\sqrt 2 }}{2}$.
Xác định hình dạng tam giác $ABC$ biết $\left\{ \begin{array}{l}\dfrac{{{b^3} + {c^3} - {a^3}}}{{b + c - a}} = {a^2}\\a = 2b\cos C\end{array} \right.$
Theo định lí cosin ta có ${\mathop{\rm cosC}\nolimits} = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$, thay vào đẳng thức thứ hai của hệ trên ta có
$a = 2b{\mathop{\rm cosC}\nolimits} = 2b.\dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}} \Rightarrow {a^2} = {a^2} + {b^2} - {c^2} \Leftrightarrow {b^2} - {c^2} = 0 \Leftrightarrow {b^2} = {c^2} \Rightarrow b = c$
Thay b = c vào hệ thức thứ nhất ta có $\dfrac{{2{b^3} - {a^3}}}{{2b - a}} = {a^2} \Leftrightarrow 2{b^3} - {a^3} = 2b{a^2} - {a^3} \Leftrightarrow {b^2} = {a^2} \Rightarrow a = b$
Do đó a = b = c. Vậy tam giác $ABC$ đều.
