Bài tập ôn tập chương 2

Hàm số \(y = \dfrac{{3x - 1}}{{2x - 2}}\) xác định khi và chỉ khi \(2x - 2 \ne 0\)\( \Leftrightarrow x \ne 1\).

\( \Rightarrow D = \mathbb{R}\backslash \left\{ 1 \right\}\)

Ta có \( - 2{x^2} - 6x + 3 =  - 2{\left( {x + \dfrac{3}{2}} \right)^2} + \dfrac{{15}}{2}\)

Do đó tịnh tiến đồ thị hàm số \(y =  - 2{x^2}\) để được đồ thị hàm số \(y =  - 2{x^2} - 6x + 3\) ta làm như sau

Tịnh tiến liên tiếp đồ thị hàm số \(y =  - 2{x^2}\) đi sang bên trái \(\dfrac{3}{2}\) đơn vị và lên trên đi \(\dfrac{{15}}{2}\) đơn vị.

Gọi hàm số cần tìm là \(y = ax + b,\,a \ne 0\)

Vì \(A \in d\) và \(B \in d\) nên ta có hệ phương trình

\(\left\{ {\begin{array}{*{20}{c}}{3 = a + b}\\{ - 1 = 2a + b}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a =  - 4}\\{b = 7}\end{array}} \right.\)

Vậy hàm số cần tìm là \(y =  - 4x + 7\)

Ta có \(\Delta :y = \dfrac{3}{2}x + \dfrac{1}{2}\). Vì ${\rm{d}}//\Delta $ nên \(\left\{ {\begin{array}{*{20}{c}}{a = \dfrac{3}{2}}\\{b \ne \dfrac{1}{2}}\end{array}} \right.\)  (1)

Mặt khác \(C \in d \Rightarrow  - 2 = 3a + b\) (2)

Từ (1) và (2) suy ra \(\left\{ {\begin{array}{*{20}{c}}{a = \dfrac{3}{2}}\\{b =  - \dfrac{{13}}{2}}\end{array}} \right.\)

Vậy hàm số cần tìm là \(y = \dfrac{3}{2}x - \dfrac{{13}}{2}\)

Đường thẳng $d$ cắt tia $Ox$ tại \(P\left( { - \dfrac{b}{a};0} \right)\) và cắt tia ${\rm{O}}y$ tại \(Q\left( {0;b} \right)\) với \(a < 0,b > 0\)

Suy ra  \({S_{\Delta OPQ}} = \dfrac{1}{2}OP.OQ = \dfrac{1}{2}.\left| { - \dfrac{b}{a}} \right|.\left| b \right| =  - \dfrac{{{b^2}}}{{2a}}\) (1)

Ta có \(M \in d \Rightarrow 2 = a + b \Rightarrow b = 2 - a\) thay vào (1) ta được

${S_{\Delta OPQ}} =  - \dfrac{{{{\left( {2 - a} \right)}^2}}}{{2a}} =  - \dfrac{2}{a} - \dfrac{a}{2} + 2$

Áp dụng bất đẳng thức Cô - si cho hai số dương $- \dfrac{2}{a}$ và $ - \dfrac{a}{2}$ ta có:                        

$ - \dfrac{2}{a} - \dfrac{a}{2} \ge 2\sqrt {\left( { - \dfrac{2}{a}} \right).\left( { - \dfrac{a}{2}} \right)}  = 2 \Rightarrow {S_{\Delta OPQ}} \ge 4$

Đẳng thức xảy ra khi và chỉ khi \(\left\{ {\begin{array}{*{20}{c}}{ - \dfrac{2}{a} =  - \dfrac{a}{2}}\\{a < 0}\end{array}} \right. \Leftrightarrow a =  - 2 \Rightarrow b = 4\)

Vậy hàm số cần tìm là \(y =  - 2x + 4\).

Đường thẳng \(d\) đi qua \(N\left( {2; - 1} \right)\) nên \( - 1 = 2a + b\) (1)

Và \(d \bot d' \Rightarrow 4.a =  - 1 \Leftrightarrow a =  - \dfrac{1}{4}\) thay vào (1) ta được \(b =  - \dfrac{1}{2}\).

Vậy hàm số cần tìm là \(y =  - \dfrac{1}{4}x - \dfrac{1}{2}\).

Ta có \({a_d} = 1 \ne {a_{d'}} = 3\) suy ra hai đường thẳng \(d,\,\,d'\)cắt nhau.

Tọa độ giao điểm của hai đường thẳng \(d,\,\,d'\) là nghiệm của hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{y = x + 2m}\\{y = 3x + 2}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = m - 1}\\{y = 3m - 1}\end{array}} \right.\)  suy ra \(d,\,\,d'\) cắt nhau tại\(M\left( {m - 1;3m - 1} \right)\)

Vì ba đường thẳng \(d,\,\,d',\,\,d''\) đồng quy nên \(M \in d''\) ta có \(3m - 1 =  - m\left( {m - 1} \right) + 2 \Leftrightarrow {m^2} + 2m - 3 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 1}\\{m =  - 3}\end{array}} \right.\)

\( \bullet \) Với \(m = 1\) ta có ba đường thẳng là \(\,\,d:y = x + 2,\,\,d':y = 3x + 2,\,\,d'':y =  - x + 2,\) phân biệt và đồng quy tại \(M\left( {0;2} \right)\).

\( \bullet \) Với \(m =  - 3\) ta có $d' \equiv d''$ suy ra \(m =  - 3\) không thỏa mãn

Vậy \(m = 1\) là giá trị cần tìm.

Với \(m = 1\) ta có $d:\,\,y = 1,\,\,d':y = 6$ do đó hai đường thẳng này song song với nhau

Với \(m =  - 1\) ta có $d:\,\,y =  - 2x - 1,\,\,d':y = 6$ suy ra hai đường thẳng này cắt nhau tại \(M\left( { - \dfrac{7}{2};6} \right)\)(loại)

Với \(m \ne  \pm 1\) khi đó hai đường thẳng trên là đồ thị của hàm số bậc nhất nên song song với nhau khi và chỉ khi \(\left\{ {\begin{array}{*{20}{c}}{m - 1 = {m^2} - 1}\\{m \ne 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left[ {\begin{array}{*{20}{c}}{m = 1}\\{m = 0}\end{array}} \right.}\\{m \ne 6}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m = 1}\\{m = 0}\end{array}} \right.\)

Đối chiếu với điều kiện \(m \ne  \pm 1\) suy ra \(m = 0\).

Vậy \(m = 0\) và \(m = 1\) là giá trị cần tìm.

Ta có tọa độ điểm \(A\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{y = \left( {m - 1} \right)x + m}\\{x = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = 0}\\{y = m}\end{array}} \right. \Rightarrow A\left( {0;m} \right)\)

Tọa độ điểm \(B\) là nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{y = \left( {{m^2} - 1} \right)x + 6}\\{y = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{\left( {{m^2} - 1} \right)x + 6 = 0}\\{y = 0}\end{array}} \right.\) (*)

Rõ ràng \(m =  \pm 1\) hệ phương trình (*) vô nghiệm

Với \(m \ne  \pm 1\) ta có (*)\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x = \dfrac{6}{{1 - {m^2}}}}\\{y = 0}\end{array}} \right. \Rightarrow B\left( {\dfrac{6}{{1 - {m^2}}};0} \right)\)

Do đó tam giác $OAB$ cân tại \(O \Leftrightarrow \left| m \right| = \left| {\dfrac{6}{{1 - {m^2}}}} \right|\)

\( \Leftrightarrow \left| {m - {m^3}} \right| = 6 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m - {m^3} = 6}\\{m - {m^3} =  - 6}\end{array}} \right.\)

\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{{m^3} - m + 6 = 0}\\{{m^3} - m - 6 = 0}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m =  - 2}\\{m = 2}\end{array}} \right.\) (thỏa mãn)

Vậy \(m =  \pm 2\) là giá trị cần tìm.

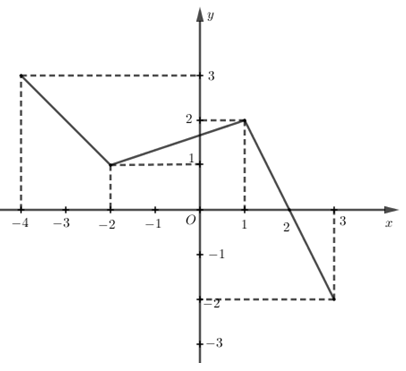
Dựa vào đồ thị hàm số đã cho ta có

$\mathop {{\rm{max}}}\limits_{\left[ { - 4;2} \right]}  = 3$  khi và chỉ khi \(x =  - 4\)

$\mathop {\min }\limits_{\left[ { - 4;2} \right]}  = 0$ khi và chỉ khi \(x = 2\)

Vậy tổng hai giá trị đó là: \(3 + 0 = 3\)

Vì \(A \in \left( P \right)\) nên \(3 = 4a + 2b + c\) (1).

Mặt khác \(\left( P \right)\) có đỉnh \(I(1;2)\) nên \( - \dfrac{b}{{2a}} = 1 \Leftrightarrow 2a + b = 0\) (2) và \(I \in \left( P \right)\) suy ra \(2 = a + b + c\) (3)

Từ (1), (2) và (3) ta có \(\left\{ \begin{array}{l}4a + 2b + c = 3\\2a + b = 0\\a + b + c = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 2\\c = 3\end{array} \right.\)

Vậy \(\left( P \right)\) cần tìm là $y = {x^2} - 2x + 3$.

Ta có \(c = 2\) và \(\left( P \right)\) đi qua \(B\left( {3; - 4} \right)\) nên \( - 4 = 9a + 3b + 2 \Leftrightarrow 3a + b =  - 2\) (*)

\(\left( P \right)\) có trục đối xứng là $x =  - \dfrac{3}{2}$ nên \( - \dfrac{b}{{2a}} =  - \dfrac{3}{2} \Leftrightarrow b = 3a\) thay vào (*) ta được \(3a + 3a =  - 2 \Leftrightarrow a =  - \dfrac{1}{3} \Rightarrow b =  - 1\) .

Vậy \(\left( P \right)\) cần tìm là $y =  - \dfrac{1}{3}{x^2} - x + 2$.

Hàm số \(y = a{x^2} + bx + c\) có giá trị nhỏ nhất bằng \(\dfrac{3}{4}\) khi \(x = \dfrac{1}{2}\) nên ta có

\( - \dfrac{b}{{2a}} = \dfrac{1}{2} \Leftrightarrow a + b = 0\) (5)

\(\dfrac{3}{4} = a{\left( {\dfrac{1}{2}} \right)^2} + b\left( {\dfrac{1}{2}} \right) + c \) \(\Leftrightarrow a + 2b + 4c = 3\) (6) và $a > 0$

Hàm số \(y = a{x^2} + bx + c\) nhận giá trị bằng \(1\) khi $x = 1$ nên \(a + b + c = 1\)(7)

Từ (5), (6) và (7) ta có \(\left\{ \begin{array}{l}a + b = 0\\a + 2b + 4c = 3\\a + b + c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b =  - 1\\c = 1\end{array} \right.\)

Vậy phương trình \(\left( P \right)\) cần tìm là $y = {x^2} - x + 1$.

Parabol cắt \(Ox\) tại điểm có hoành độ bằng \(2\) suy ra \(\left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right.\)

Ta có: \(0 = a{.2^2} + 3.2 - 2 \Leftrightarrow a =  - 1\)

Vậy parabol \(y =  - {x^2} + 3x - 2\)

Ta có \( - \dfrac{b}{{2a}} = 3,\,\, - \dfrac{\Delta }{{4a}} =  - 1\)

Bảng biến thiên

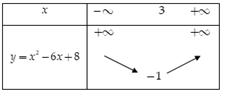
Suy ra đồ thị hàm số \(y = {x^2} - 6x + 8\) có đỉnh là \(I\left( {3; - 1} \right)\), đi qua các điểm \(A\left( {2;0} \right),\,\,B\left( {4;0} \right)\)

Nhận đường thẳng $x = 3$ làm trục đối xứng và hướng bề lõm lên trên.

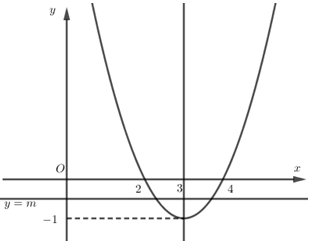
Đường thẳng \(y = m\left( { - 1 < m < 0} \right)\) song song với trục hoành nên ta thấy đường thẳng cắt đồ thị tại \(2\) điểm phân biệt.

Ta có \( - \dfrac{b}{{2a}} =  - 1,\,\, - \dfrac{\Delta }{{4a}} = 4\)

Bảng biến thiên

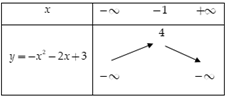
Suy ra đồ thị hàm số \(y =  - {x^2} - 2x + 3\) có đỉnh là \(I\left( { - 1;4} \right)\), đi qua các điểm \(A\left( {1;0} \right),\,\,B\left( { - 3;0} \right)\)

Nhận đường thẳng $x =  - 1$ làm trục đối xứng và hướng bề lõm xuống dưới.

Trên đoạn \(\left[ { - 3;1} \right]\)thì hàm số đạt GTNN \(y = 0\)

Ta có \(\Delta ' = {\left( {m + 3} \right)^2} - \left( {{m^2} - 3} \right) = 6m + 12\)

Phương trình có nghiệm \( \Leftrightarrow \Delta ' \ge 0 \Leftrightarrow 6m + 12 \ge 0 \Leftrightarrow m \ge  - 2\)

Theo định lý Viét ta có \(\left\{ {\begin{array}{*{20}{c}}{{x_1} + {x_2} =  - 2\left( {m + 3} \right)}\\{{x_1}{x_2} = {m^2} - 3}\end{array}} \right.\)

\(P =  - 10\left( {m + 3} \right) - 2\left( {{m^2} - 3} \right) =  - 2{m^2} - 10m - 24\)

Xét hàm số \(y =  - 2{x^2} - 10x - 24\) với $x \in \left[ { - 2; + \infty } \right)$

Bảng biến thiên

Suy ra \(\mathop {max}\limits_{\left[ { - 2; + \infty } \right)} y =  - 12\) khi và chỉ khi $x =  - 2$

Vậy \(m =  - 2\) là giá trị cần tìm.

ĐKXĐ: \(\left\{ {\begin{array}{*{20}{c}}{4x + 5 \ge 0}\\{x - 1 \ge 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ge  - \dfrac{5}{4}}\\{x \ge 1}\end{array}} \right. \Leftrightarrow x \ge 1\)

Suy ra TXĐ: ${\rm{D}} = \left[ {1; + \infty } \right)$

Với mọi ${x_1},\,{x_2} \in \left[ {1; + \infty } \right),\,\,{x_1} \ne {x_2}$ ta có

\(\begin{array}{l}f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = \sqrt {4{x_2} + 5}  + \sqrt {{x_2} - 1}  - \sqrt {4{x_1} + 5}  - \sqrt {{x_1} - 1} \\ = \dfrac{{4\left( {{x_2} - {x_1}} \right)}}{{\sqrt {4{x_2} + 5}  + \sqrt {4{x_1} + 5} }} + \dfrac{{{x_2} - {x_1}}}{{\sqrt {{x_2} - 1}  + \sqrt {{x_1} - 1} }}\\ = \left( {{x_2} - {x_1}} \right)\left( {\dfrac{4}{{\sqrt {4{x_2} + 5}  + \sqrt {4{x_1} + 5} }} + \dfrac{1}{{\sqrt {{x_2} - 1}  + \sqrt {{x_1} - 1} }}} \right)\end{array}\)

Suy ra \(\dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \dfrac{4}{{\sqrt {4{x_2} + 5}  + \sqrt {4{x_1} + 5} }} + \dfrac{1}{{\sqrt {{x_2} - 1}  + \sqrt {{x_1} - 1} }} > 0\)

Nên hàm số \(y = \sqrt {4x + 5}  + \sqrt {x - 1} \) đồng biến trên khoảng $\left[ {1; + \infty } \right)$.

Vì hàm số đã cho đồng biến trên $\left[ {1; + \infty } \right)$ nên

Nếu \(x > 1 \Rightarrow f\left( x \right) > f\left( 1 \right)\) hay  \(\sqrt {4x + 5}  + \sqrt {x - 1}  > 3\)

Suy ra phương trình \(\sqrt {4x + 5}  + \sqrt {x - 1}  = 3\) vô nghiệm

Nếu $x < 1 \Rightarrow f\left( x \right) < f\left( 1 \right)$ hay  \(\sqrt {4x + 5}  + \sqrt {x - 1}  < 3\)

Suy ra phương trình \(\sqrt {4x + 5}  + \sqrt {x - 1}  = 3\) vô nghiệm

Với \(x = 1\) dễ thấy nó là nghiệm của phương trình đã cho

Vậy phương trình có nghiệm duy nhất $x = 1$.

ĐKXĐ: \(\left\{ {\begin{array}{*{20}{c}}{4x + 5 \ge 0}\\{x - 1 \ge 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{x \ge  - \dfrac{5}{4}}\\{x \ge 1}\end{array}} \right. \Leftrightarrow x \ge 1\)

Suy ra TXĐ: ${\rm{D}} = \left[ {1; + \infty } \right)$

Với mọi ${x_1},\,{x_2} \in \left[ {1; + \infty } \right),\,\,{x_1} \ne {x_2}$ ta có

\(\begin{array}{l}f\left( {{x_2}} \right) - f\left( {{x_1}} \right) = \sqrt {4{x_2} + 5}  + \sqrt {{x_2} - 1}  - \sqrt {4{x_1} + 5}  - \sqrt {{x_1} - 1} \\ = \dfrac{{4\left( {{x_2} - {x_1}} \right)}}{{\sqrt {4{x_2} + 5}  + \sqrt {4{x_1} + 5} }} + \dfrac{{{x_2} - {x_1}}}{{\sqrt {{x_2} - 1}  + \sqrt {{x_1} - 1} }}\\ = \left( {{x_2} - {x_1}} \right)\left( {\dfrac{4}{{\sqrt {4{x_2} + 5}  + \sqrt {4{x_1} + 5} }} + \dfrac{1}{{\sqrt {{x_2} - 1}  + \sqrt {{x_1} - 1} }}} \right)\end{array}\)

Suy ra \(\dfrac{{f\left( {{x_2}} \right) - f\left( {{x_1}} \right)}}{{{x_2} - {x_1}}} = \dfrac{4}{{\sqrt {4{x_2} + 5}  + \sqrt {4{x_1} + 5} }} + \dfrac{1}{{\sqrt {{x_2} - 1}  + \sqrt {{x_1} - 1} }} > 0\)

Nên hàm số \(y = \sqrt {4x + 5}  + \sqrt {x - 1} \) đồng biến trên khoảng $\left[ {1; + \infty } \right)$.

Xét phương trình đã cho:

Đặt ${x^2} + 1 = t,\,\,t \ge 1 \Rightarrow {x^2} = t - 1$  phương trình trở thành

\(\sqrt {4x + 5}  + \sqrt {x - 1}  = \sqrt {4t + 5}  + \sqrt {t - 1}  \Leftrightarrow f\left( x \right) = f\left( t \right)\)

Nếu \(x > t \Rightarrow f\left( x \right) > f\left( t \right)\) hay  \(\sqrt {4x + 5}  + \sqrt {x - 1}  > \sqrt {4t + 5}  + \sqrt {t - 1} \)

Suy ra phương trình đã cho vô nghiệm

Nếu $x < t \Rightarrow f\left( x \right) < f\left( t \right)$ hay  \(\sqrt {4x + 5}  + \sqrt {x - 1}  < \sqrt {4t + 5}  + \sqrt {t - 1} \)

Suy ra phương trình đã cho vô nghiệm

Vậy \(f\left( x \right) = f\left( t \right) \Leftrightarrow x = t\) hay ${x^2} + 1 = x \Leftrightarrow {x^2} - x + 1 = 0$ (vô nghiệm)

Vậy phương trình đã cho vô nghiệm.

Gọi \(M,N\) đối xứng nhau qua gốc tọa độ \(O\). \(M\left( {{x_0};{y_0}} \right) \Rightarrow N\left( { - {x_0}; - {y_0}} \right)\)

Vì $M,{\rm{ }}N$ thuộc đồ thị hàm số nên \(\left\{ {\begin{array}{*{20}{c}}{{y_0} =  - x_0^3 + x_0^2 + 3{x_0} - 4}\\{ - {y_0} = x_0^3 + x_0^2 - 3{x_0} - 4}\end{array}} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{y_0} =  - x_0^3 + x_0^2 + 3{x_0} - 4}\\{2x_0^2 - 8 = 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{y_0} =  - x_0^3 + x_0^2 + 3{x_0} - 4}\\{{x_0} =  \pm 2}\end{array}} \right.\)

\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{{x_0} = 2}\\{{y_0} =  - 2}\end{array}} \right.\) hoặc \(\left\{ {\begin{array}{*{20}{c}}{{x_0} =  - 2}\\{{y_0} = 2}\end{array}} \right.\)

Vậy hai điểm cần tìm có tọa độ là \(\left( {2; - 2} \right)\) và \(\left( { - 2;2} \right)\).