Cho hàm số \(y = 3\left| {x - 2} \right| - \left| {2x - 6} \right|\) có đồ thị \((C)\). Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên với \(x \in \left[ { - 3;4} \right]\)
Ta có \(y = \left\{ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 3\\5x - 12\,\,\,\,khi\,\,2 < x < 3\\ - x\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \le 2\end{array} \right.\)
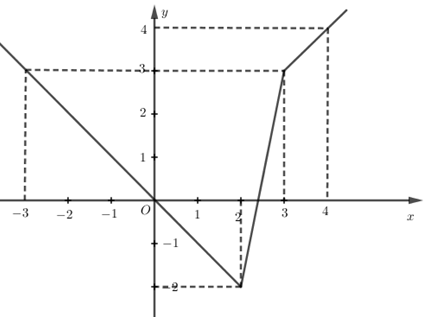
Vẽ đường thẳng \(y = x\) đi qua hai điểm \(O\left( {0;0} \right),\,\,A\left( {1;1} \right)\) và lấy phần đường thẳng bên phải của đường thẳng $x = 3$
Vẽ đường thẳng \(y = 5x - 12\) đi qua hai điểm \(B\left( {3;3} \right),\,\,C\left( {2; - 2} \right)\) và lấy phần đường thẳng nằm giữa của hai đường thẳng $x = 2,\,\,x = 3$.
Vẽ đường thẳng \(y = - x\) đi qua hai điểm \(O\left( {0;0} \right),\,\,D\left( { - 1; - 1} \right)\) và lấy phần đường thẳng bên trái của đường thẳng $x = 2$
Dựa vào đồ thị hàm số ta có:
\(\mathop {{\rm{max}}}\limits_{\left[ { - 3;4} \right]} y = 4\) khi và chỉ khi $x = 4$
\(\mathop {\min y}\limits_{\left[ { - 3;4} \right]} = - 2\) khi và chỉ khi $x = 2$
Cho hàm số $f\left( x \right) = \left| {2x - m} \right|$. Tìm $m$ để giá trị lớn nhất của \(f\left( x \right)\) trên $\left[ {1;2} \right]$ đạt giá trị nhỏ nhất.
Dựa vào các nhận xét trên ta thấy $\mathop {\max }\limits_{[1;\,2]} f(x)$ chỉ có thể đạt được tại \(x = 1\) hoặc $x = 2$ .
Như vậy nếu đặt $M = \mathop {\max }\limits_{[1;\,2]} f(x)$ thì $M \ge f\left( 1 \right) = \left| {2 - m} \right|$ và $M \ge f\left( 2 \right) = \left| {4 - m} \right|$.
Ta có
$M \ge \dfrac{{f(1) + f(2)}}{2} = \dfrac{{\left| {2 - m} \right| + \left| {4 - m} \right|}}{2} $ $\ge \dfrac{{\left| {(2 - m) + (m - 4)} \right|}}{2} = 1$
Đẳng thức xảy ra khi và chỉ khi $\left\{ \begin{array}{l}\left| {2 - m} \right| = \left| {4 - m} \right|\\(2 - m)(m - 4) \ge 0\end{array} \right. \Leftrightarrow m = 3$.
Vậy giá trị nhỏ nhất của $M$ là $1,$ đạt được chỉ khi $m = 3.$
Xác định parabol \(\left( P \right)\): \(y = a{x^2} + bx + c\), \(a \ne 0\) đỉnh \(I\) biết \(\left( P \right)\) đi qua \(M(4;3)\) cắt \(Ox\) tại \(N(3;0)\) và \(P\) sao cho \(\Delta INP\) có diện tích bằng $1$, biết hoành độ điểm \(P\) nhỏ hơn \(3\).
Vì \(\left( P \right)\) đi qua \(M(4;3)\) nên \(3 = 16a + 4b + c\) (1)
Mặt khác \(\left( P \right)\) cắt \(Ox\) tại \(N(3;0)\) suy ra \(0 = 9a + 3b + c\) (2), \(\left( P \right)\) cắt \(Ox\) tại \(P\) nên \(P\left( {t;0} \right),\,\,t < 3\)
Theo định lý Viét ta có \(\left\{ {\begin{array}{*{20}{c}}{t + 3 = - \dfrac{b}{a}}\\{3t = \dfrac{c}{a}}\end{array}} \right.\)
Ta có \({S_{\Delta IPN}} = \dfrac{1}{2}IH.NP\) với \(H\) là hình chiếu của \(I\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\) lên $PN$ hay trục hoành
Do \(IH = \left| { - \dfrac{\Delta }{{4a}}} \right|\), \(NP = 3 - t\) nên \({S_{\Delta INP}} = 1 \Leftrightarrow \dfrac{1}{2}\left| { - \dfrac{\Delta }{{4a}}} \right|.\left( {3 - t} \right) = 1\)
\( \Leftrightarrow \left( {3 - t} \right)\left| {{{\left( {\dfrac{b}{{2a}}} \right)}^2} - \dfrac{c}{a}} \right| = \left| {\dfrac{2}{a}} \right| \Leftrightarrow \left( {3 - t} \right)\left| {{{\dfrac{{\left( {t + 3} \right)}}{4}}^2} - 3t} \right| = \left| {\dfrac{2}{a}} \right| \Leftrightarrow {\left( {3 - t} \right)^3} = \dfrac{8}{{\left| a \right|}}\) (3)
Từ (1) và (2) ta có \(7a + b = 3 \Leftrightarrow b = 3 - 7a\) suy ra \(t + 3 = - \dfrac{{3 - 7a}}{a} \Leftrightarrow \dfrac{1}{a} = \dfrac{{4 - t}}{3}>0\) do $t<3$
Thay vào (3) ta có \({\left( {3 - t} \right)^3} = \dfrac{{8\left( {4 - t} \right)}}{3} \Leftrightarrow 3{t^3} - 27{t^2} + 73t - 49 = 0 \Leftrightarrow t = 1\)
Suy ra $a = 1 \Rightarrow b = - 4 \Rightarrow c = 3$.
Vậy \(\left( P \right)\) cần tìm là $y = {x^2} - 4x + 3$.
Tìm giá trị nhỏ nhất của hàm số: \(y = \sqrt[3]{{{x^4} + 2{x^2} + 1}} - 3\sqrt[3]{{{x^2} + 1}} + 1\)
Đặt \(t = \sqrt[3]{{{x^2} + 1}},\,\,t \ge 1 \Rightarrow {t^2} = \sqrt[3]{{{x^4} + 2{x^2} + 1}}\)
Khi đó hàm số trở thành \(y = {t^2} - 3t + 1\) với \(t \ge 1\).
Bảng biến thiên
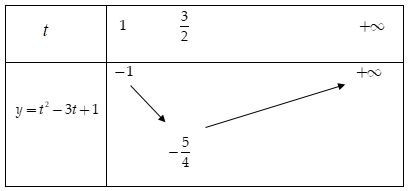
Suy ra giá trị nhỏ nhất của hàm số \(y = \sqrt[3]{{{x^4} + 2{x^2} + 1}} - 3\sqrt[3]{{{x^2} + 1}} + 1\) là \( - \dfrac{5}{4}\) khi và chỉ khi $t = \dfrac{3}{2}$ hay \(\sqrt[3]{{{x^2} + 1}} = \dfrac{3}{2} \Leftrightarrow x = \pm \sqrt {\dfrac{{19}}{8}} \)
Tìm m để hàm số \(y = \left( {m - 2} \right)x + 5\) thỏa mãn \(y > 0\forall x \in \left[ {0;2} \right] \)
\(y > 0\forall x \in \left[ {0;2} \right] \Leftrightarrow \left( {m - 2} \right)x + 5 > 0\forall x \in \left[ {0;2} \right]\)(1)
TH1: \(m - 2 \ge 0 \Leftrightarrow m \ge 2\)
\( \Rightarrow \left( {m - 2} \right)x + 5 \ge 0 + 5 = 5 > 0\forall x \in \left[ {0;2} \right]\)
TH2: \(m - 2 < 0 \Leftrightarrow m < 2\)
\(\begin{array}{l}(1) \Leftrightarrow x < - \dfrac{5}{{m - 2}}\forall x \in \left[ {0;2} \right]\\ \Leftrightarrow 2 < - \dfrac{5}{{m - 2}} \Leftrightarrow \dfrac{{2m + 1}}{{m - 2}} < 0\\ \Leftrightarrow - \dfrac{1}{2} < m < 2\end{array}\)
Vậy \(m > - \dfrac{1}{2}\) thì \(y > 0\)
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \({x^2} - 3x + 2 - m = 0\) có nghiệm trên đoạn \(\left[ { - 1;2} \right]\) ?
\({x^2} - 3x + 2 - m = 0 \Rightarrow m = {x^2} - 3x + 2\,\,\,\left( 1 \right)\)
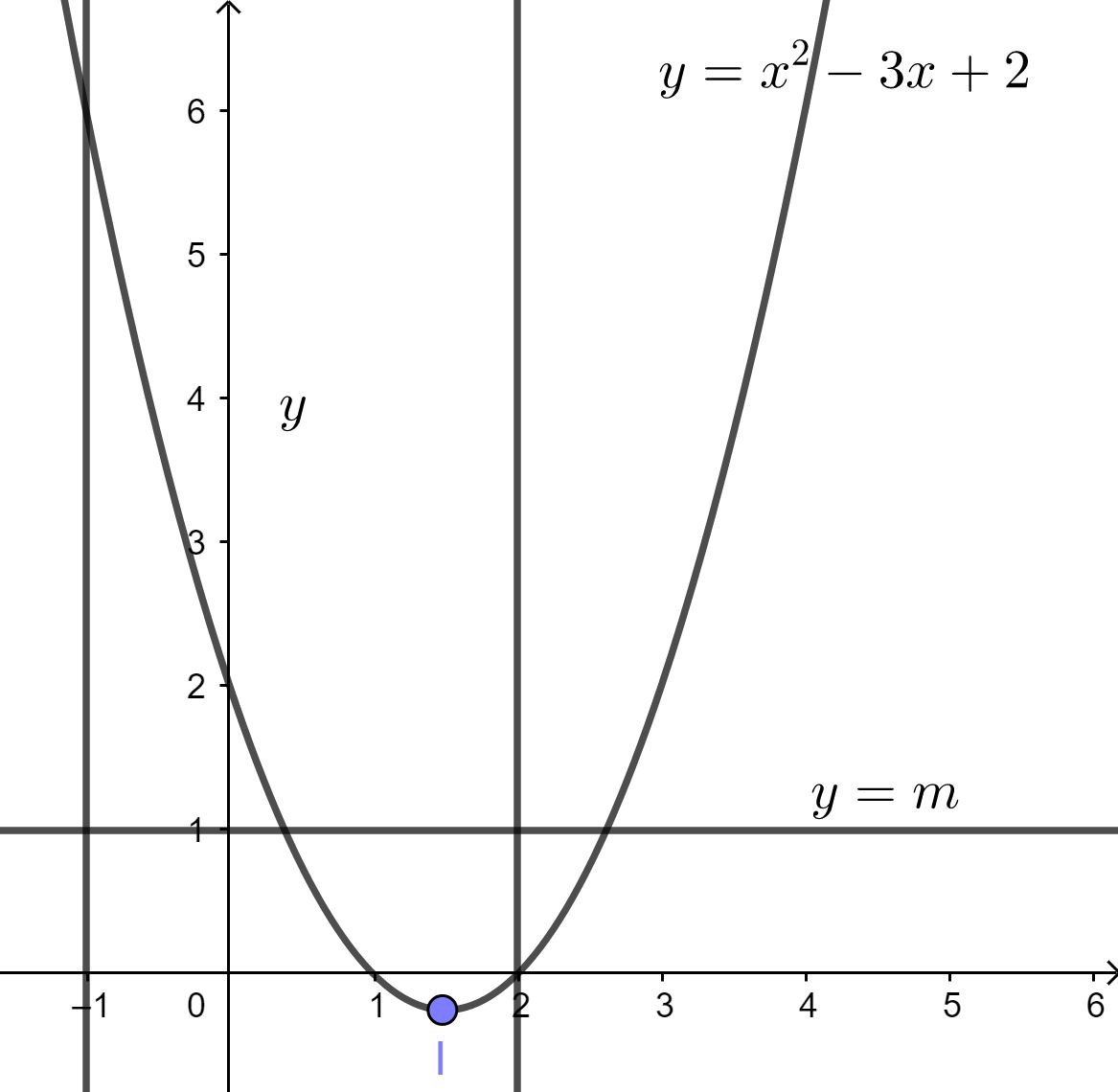
Số nghiệm của phương trình (1) trên \(\left[ { - 1;2} \right]\) là số giao điểm của đồ thị hàm số \(y = {x^2} - 3x + 2\) với đường thẳng \(y = m\) song song \(Ox\) trên \(\left[ { - 1;2} \right]\)
Đồ thị có đỉnh \(I\left( {\dfrac{3}{2};\dfrac{{ - 1}}{4}} \right)\)
\(f\left( { - 1} \right) = 6;f\left( 2 \right) = 0\)
Để phương trình (1) có nghiệm thì \(\dfrac{{ - 1}}{4} \le m \le 6\). Do \(m \in \mathbb{Z} \Rightarrow m \in \left\{ {0;1;2;3;4;5;6} \right\}\)
Tìm tất cả các giao điểm của parabola \(\left( P \right):y = 2{x^2} - x + 2\) với đường thẳng \(d:y = 3\).
Xét phương trình hoành độ giao điểm ta có: \(2{x^2} - x + 2 = 3 \Leftrightarrow 2{x^2} - x - 1 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \dfrac{{ - 1}}{2}\end{array} \right.\)
Vậy tọa độ giao điểm là \(\left( {1;3} \right),\left( { - \dfrac{1}{2};3} \right)\)
Hàm số \(y = \left( {m - 5} \right){x^2} - 5x + 1\) là hàm số bậc nhất
\( \Leftrightarrow m - 5 = 0 \Leftrightarrow m = 5\).

