Câu hỏi:
2 năm trước
Tìm giá trị nhỏ nhất của hàm số: \(y = \sqrt[3]{{{x^4} + 2{x^2} + 1}} - 3\sqrt[3]{{{x^2} + 1}} + 1\)
Trả lời bởi giáo viên
Đáp án đúng: c
Đặt \(t = \sqrt[3]{{{x^2} + 1}},\,\,t \ge 1 \Rightarrow {t^2} = \sqrt[3]{{{x^4} + 2{x^2} + 1}}\)
Khi đó hàm số trở thành \(y = {t^2} - 3t + 1\) với \(t \ge 1\).
Bảng biến thiên
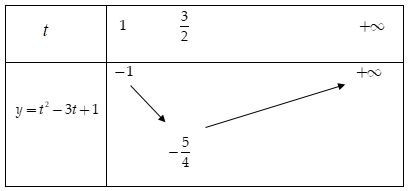
Suy ra giá trị nhỏ nhất của hàm số \(y = \sqrt[3]{{{x^4} + 2{x^2} + 1}} - 3\sqrt[3]{{{x^2} + 1}} + 1\) là \( - \dfrac{5}{4}\) khi và chỉ khi $t = \dfrac{3}{2}$ hay \(\sqrt[3]{{{x^2} + 1}} = \dfrac{3}{2} \Leftrightarrow x = \pm \sqrt {\dfrac{{19}}{8}} \)
Hướng dẫn giải:
- Đặt \(t = \sqrt[3]{{{x^2} + 1}}\) tìm điều kiện của \(t\)
- Đưa hàm số về hàm số bậc hai ẩn \(t\)
- Tìm GTNN của hàm số theo điều kiện của \(t\) đã đặt.
