Câu hỏi:
2 năm trước
Cho hàm số \(y = - {x^2} - 2x + 3\). Hãy tìm giá trị nhỏ nhất của hàm số đã cho trên \(\left[ { - 3;1} \right]\).
Trả lời bởi giáo viên
Đáp án đúng: b
Ta có \( - \dfrac{b}{{2a}} = - 1,\,\, - \dfrac{\Delta }{{4a}} = 4\)
Bảng biến thiên
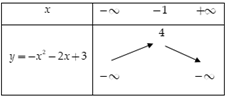
Suy ra đồ thị hàm số \(y = - {x^2} - 2x + 3\) có đỉnh là \(I\left( { - 1;4} \right)\), đi qua các điểm \(A\left( {1;0} \right),\,\,B\left( { - 3;0} \right)\)
Nhận đường thẳng $x = - 1$ làm trục đối xứng và hướng bề lõm xuống dưới.

Trên đoạn \(\left[ { - 3;1} \right]\)thì hàm số đạt GTNN \(y = 0\)
Hướng dẫn giải:
- Vẽ đồ thị hàm số.
- Dựa vào đồ thị tìm GTNN của hàm số trên đoạn \(\left[ { - 3;1} \right]\)

