Cho $3$ đường thẳng \(\left( {{d_1}} \right)\):\(3x - 2y + 5 = 0\), \(\left( {{d_2}} \right)\):\(2x + 4y - 7 = 0\), \(\left( {{d_3}} \right)\): \(3x + 4y - 1 = 0\). Viết phương trình đường thẳng $\left( d \right)$ đi qua giao điểm của \(\left( {{d_1}} \right)\), \(\left( {{d_2}} \right)\) và song song với \(\left( {{d_3}} \right)\).
Tọa độ giao điểm $M$ của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là nghiệm của hệ $\left\{ \begin{array}{l}3x - 2y = - 5\\2x + 4y = 7\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{3}{8}\\y = \dfrac{{31}}{{16}}\end{array} \right.$$ \Rightarrow M\left( { - \dfrac{3}{8};\dfrac{{31}}{{16}}} \right)$.
Phương trình đường thẳng $\left( \Delta \right)$ song song với \(\left( {{d_3}} \right)\) qua $M\left( { - \dfrac{3}{8};\dfrac{{31}}{{16}}} \right)$ có dạng
\(\left( \Delta \right)\): \(3\left( {x + \dfrac{3}{8}} \right) + 4\left( {y - \dfrac{{31}}{{16}}} \right) = 0\)\( \Leftrightarrow 3x + 4y - \dfrac{{53}}{8} = 0\)\( \Leftrightarrow 24x + 32y - 53 = 0\).
Trong mặt phẳng tọa độ \(Oxy\), hình chiếu vuông góc của điểm \(A\left( {2;1} \right)\) lên đường thẳng \(d\): \(2x + y - 7 = 0\) có tọa độ là.
Đường thẳng \(\left( \Delta \right)\) vuông góc với \(d\) có phương trình: \(x - 2y +m= 0\).
\(\left( \Delta \right)\) đi qua \(A\left( {2;1} \right)\) nên:
\(2-2.1+m=0\Leftrightarrow m=0\)
Do đó \(\left( \Delta \right)\):\(x-2y=0\).
Gọi \(A'\) là hình chiếu của \(A\) lên \(d\) khi đó \(A' = \Delta \cap d\).
Tọa độ \(A\) là nghiệm hệ phương trình:
\(\left\{ \begin{array}{l}2x + y - 7 = 0\\x - 2y = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{14}}{5}\\y = \dfrac{7}{5}\end{array} \right.\).
Vậy \(A'\left( {\dfrac{{14}}{5};\dfrac{7}{5}} \right)\).
Cho đường thẳng \(d:x - 2y - 3 = 0\). Tìm tọa độ hình chiếu vuông góc \(H\) của điểm \(M\left( {\,0;\,1} \right)\) trên đường thẳng.
\(\Delta \bot d \Rightarrow \Delta :2x + y + m = 0\), mà \(M\left( {\,0;\,1} \right) \in \Delta :\)\(2.0 + 1 + m = 0\)\( \Leftrightarrow m = - 1\)\( \Rightarrow \Delta :2x + y - 1 = 0\).
Tọa độ điểm \(H\) là nghiệm của hệ: \(\left\{ \begin{array}{l}2x + y - 1 = 0\\x - 2y - 3 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = - 1\end{array} \right.\).
Vậy \(H\left( {\,1;\, - 1} \right)\).
Trong mặt phẳng tọa độ \(Oxy\) cho hai điểm \(M\left( {4;1} \right)\), \(N\left( { - 1;2} \right)\), \(M'\left( {x;y} \right)\) là điểm đối xứng với \(M\) qua \(N\). Khi đó \(x + y\) có giá trị là
Ta có \(M'\left( {x;y} \right)\) là điểm đối xứng với \(M\) qua \(N\) nên \(N\) là trung điểm \(MM'\).
Tọa độ điểm \(M'\) là \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_N} - {x_M}\\{y_{M'}} = 2{y_N} - {y_M}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_{M'}} = - 6\\{y_{M'}} = 3\end{array} \right.\).
Vậy \(x + y = - 3\).
Trong mặt phẳng với hệ tọa độ \(Oxy\) cho đường thẳng \(d:\,x - 2y + 1 = 0\) và điểm \(M\left( {2;\,3} \right)\). Phương trình đường thẳng \(\Delta \) đi qua điểm \(M\) và vuông góc với đường thẳng \(d\) là
\(\Delta \) vuông góc \(d:\,x - 2y + 1 = 0\)\( \Rightarrow \Delta \) có VTPT là \(\overrightarrow n = \left( {2;\,1} \right)\).
\(\Delta \) qua \(M\left( {2;\,3} \right)\) nên có phương trình là \(2\left( {x - 2} \right) + \left( {y - 3} \right) = 0\)\( \Leftrightarrow 2x + y - 7 = 0\).
Trong mặt phẳng với hệ tọa độ \(Oxy\) cho \(\Delta ABC\) có \(A\left( {1;\;2} \right)\), \(B\left( {4;\; - 2} \right)\), \(C\left( { - 3;\;5} \right)\). Một véctơ chỉ phương của đường phân giác trong của góc \(A\) là
Ta có \(\overrightarrow {AB} = \left( {3;\; - 4} \right)\), \(\overrightarrow {AC} = \left( { - 4;\;3} \right)\)\( \Rightarrow \left| {\overrightarrow {AB} } \right| = \left| {\overrightarrow {AC} } \right|\), suy ra \(\Delta ABC\) là tam giác cân tại \(A\).
Do đó đường phân giác trong của góc \(A\) cũng chính là đường trung tuyến của tam giác.
Gọi \(M\) là trung điểm của \(BC\) khi đó \(\overrightarrow {AM} \) là véctơ chỉ phương của đường phân giác trong của góc \(A\).
Ta có \(\left\{ \begin{array}{l}{x_M} = \dfrac{{{x_B} + {x_C}}}{2}\\{y_M} = \dfrac{{{y_B} + {y_C}}}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{{4 + \left( { - 3} \right)}}{2} = \dfrac{1}{2}\\{y_M} = \dfrac{{ - 2 + 5}}{2} = \dfrac{3}{2}\end{array} \right. \Rightarrow M\left( {\dfrac{1}{2};\;\dfrac{3}{2}} \right)\).
Suy ra \(\overrightarrow {AM} = \left( { - \dfrac{1}{2};\; - \dfrac{1}{2}} \right)\).
Vậy một véctơ chỉ phương của đường phân giác trong của góc \(A\) có dạng \(\overrightarrow u = \left( {1;\;1} \right)\).
Cho hai điểm $A\left( {1;\, - 4} \right)$, $B\left( {3;\,2} \right)$. Viết phương trình tổng quát của đường thẳng trung trực của đoạn thẳng $AB$.
Gọi $M$ là trung điểm của $AB$$ \Rightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{{{x_A} + {x_B}}}{2}\\{y_M} = \dfrac{{{y_A} + {y_B}}}{2}\end{array} \right.$$ \Rightarrow \left\{ \begin{array}{l}{x_M} = 2\\{y_M} = - 1\end{array} \right. \Rightarrow M\left( {2;\, - 1} \right)$.
Đường trung trực của đoạn thẳng \(AB\) nhận \(\overrightarrow {AB} = \left( {2;6} \right)\) làm VTPT và đi qua \(M\left( {2; - 1} \right)\) nên:
PTTQ: $2\left( {x - 2} \right) + 6\left( {y + 1} \right) = 0$$ \Leftrightarrow x + 3y + 1 = 0$.
Cho tam giác $ABC$có \(A\left( { - 2;3} \right)\,,B\left( {1; - 2} \right)\,,C\left( { - 5;4} \right).\)Đường trung tuyến $AM$ có phương trình tham số
Gọi \(M\) trung điểm \(BC\) nên \(\left\{ \begin{array}{l}
{x_M} = \frac{{{x_B} + {x_C}}}{2} = \frac{{1 - 5}}{2} = - 2\\
{y_M} = \frac{{{y_B} + {y_C}}}{2} = \frac{{ - 2 + 4}}{2} = 1
\end{array} \right.\)
\( \Rightarrow M\left( { - 2;1} \right)\)
\( \Rightarrow \overrightarrow {AM} = \left( {0; - 2} \right) \)
Đường thẳng AM đi qua A(-2;3) và nhận \( \overrightarrow {AM} = \left( {0; - 2} \right) \) làm VTCP nên có phương trình tham số là:
\(\left( {AM} \right):\left\{ \begin{array}{l}x = - 2\\y = 3 - 2t\end{array} \right.\)
Cho hai điểm $A\left( {1;\,1} \right)$, $B\left( {0;\, - 2} \right)$, $C\left( {4;\,2} \right)$. Phương trình tổng quát của đường trung tuyến đi qua điểm $A$ của tam giác $ABC$ là
Gọi $M$ là trung điểm của cạnh $BC$$ \Rightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{{{x_B} + {x_C}}}{2}\\{y_M} = \dfrac{{{y_B} + {y_C}}}{2}\end{array} \right.$$ \Rightarrow \left\{ \begin{array}{l}{x_M} = 2\\{y_M} = 0\end{array} \right. \Rightarrow M\left( {2;\,0} \right)$.
Ta có $\overrightarrow {AM} = \left( {1;\, - 1} \right)$$ \Rightarrow \overrightarrow {{n_{AM}}} = \left( {1;\,1} \right)$.
Phương trình đường trung tuyến $AM$: $\left\{ \begin{array}{l}\overrightarrow {{n_{AM}}} = \left( {1;1} \right)\\A\left( {1;1} \right)\end{array} \right.$.
PTTQ: $x + y - 2 = 0$.
Đường thẳng \(d\) qua \(A\left( {1;\;1} \right)\) và có véctơ chỉ phương \(\overrightarrow u = \left( {2;3} \right)\) có phương trình tham số là
Đường thẳng \(d\) qua \(A\left( {1;\;1} \right)\) và có véctơ chỉ phương \(\overrightarrow u = \left( {2;3} \right)\) có phương trình tham số là
\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 1 + 3t\end{array} \right.\).
Viết phương trình tham số của đường thẳng đi qua \(A\left( {3;4} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {3; - 2} \right)\)
Phương trình tham số của đường thẳng đi qua \(A\left( {3;4} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( {3; - 2} \right)\) có dạng: \(\left\{ \begin{array}{l}x = 3 + 3t\\y = 4 - 2t\end{array} \right.\).
Trong mặt phẳng tọa độ \(Oxy\), cho điểm \(A\left( {2;\;1} \right)\) và đường thẳng \(\Delta :\left\{ \begin{array}{l}x = - 1 + 2t\\y = 2 + t\end{array} \right.\). Tìm tọa độ điểm \(M\) thuộc đường thẳng \(\Delta \) sao cho \(AM = \sqrt {10} \).
Gọi \(M\left( { - 1 + 2t;\;2 + t} \right)\).
Do \(AM = \sqrt {10} \Rightarrow \sqrt {{{\left( {2t - 3} \right)}^2} + {{\left( {t + 1} \right)}^2}} = \sqrt {10} \) \( \Leftrightarrow 5{t^2} - 10t + 10 = 10 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 2\end{array} \right.\).
Với \(t = 0\)\( \Rightarrow M\left( { - 1;\;2} \right)\).
Với \(t = 2\)\( \Rightarrow M\left( {3;\;4} \right)\).
Vậy \(M\left( { - 1;\;2} \right)\) hoặc \(M\left( {3;\;4} \right)\).
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) có \(C\left( { - 1;2} \right)\), đường cao \(BH\): \(x - y + 2 = 0\), điểm \(A\) nằm trên đường thẳng \(2x - y + 5 = 0\). Tọa độ điểm \(A\) là.
Đường thẳng \(AC\) qua \(C\left( { - 1;2} \right)\)và vuông góc với \(BH\) nên có phương trình \(AC\):\(x + y - 1 = 0\)
Khi đó tọa độ điểm \(A\) là nghiệm của hệ \(\left\{ \begin{array}{l}x + y - 1 = 0\\2x - y + 5 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{4}{3}\\y = \dfrac{7}{3}\end{array} \right.\). Vậy \(A\left( { - \dfrac{4}{3};\dfrac{7}{3}} \right)\).
Cho tam giác \(ABC\) với \(A\left( {2;\,4} \right)\); \(B\left( {2;\,1} \right)\); \(C\left( {5;\,0} \right)\). Trung tuyến \(CM\) đi qua điểm nào dưới đây?
$M$ là trung điểm của \(AB\)nên \(M\left( {2;\,\dfrac{5}{2}} \right)\); \(\overrightarrow {CM} \left( { - 3;\,\dfrac{5}{2}} \right)\).
Phương trình tham số của đường thẳng \(CM\) là \(\left\{ \begin{array}{l}x = 5 - 3t\\y = \dfrac{5}{2}t\end{array} \right.\).
Với \(t = 2\) thì \(\left\{ \begin{array}{l}x = - 1\\y = 5\end{array} \right.\).
Cho tam giác \(ABC\) có \(A\left( { - 2;7} \right)\); \(B\left( {3;5} \right)\); \(C\left( {1; - 4} \right)\). Biết rằng trực tâm của tam giác \(ABC\) là điểm \(H\left( {\dfrac{a}{m};\dfrac{b}{n}} \right)\), với \(\min T = \dfrac{{\sqrt 2 }}{2}\), \(b\), $P = {x_1}{x_2} = - \dfrac{1}{2}$, $n$ là các số nguyên dương và \(\dfrac{a}{m}\), \(\dfrac{b}{n}\) là các phân số tối giản. Tính \(T = \dfrac{a}{m} + \dfrac{b}{n}.\)
Đường cao \(AH\) của \(\Delta ABC\) qua \(A\left( { - 2;7} \right)\) và nhận \(\overrightarrow {CB} = \left( {2;9} \right)\) làm VTPT nên có phương trình: \(2\left( {x + 2} \right) + 9\left( {y - 7} \right) = 0 \Leftrightarrow 2x + 9y - 59 = 0\).
Đường cao \(BH\) của \(\Delta ABC\) qua \(B\left( {3;5} \right)\) và nhận \(\overrightarrow {AC} = \left( {3; - 11} \right)\) làm VTPT nên có phương trình là \(3\left( {x - 3} \right) - 11\left( {y - 5} \right) = 0 \Leftrightarrow 3x - 11y + 46 = 0\).
Tọa độ điểm \(H\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}2x + 9y - 59 = 0\\3x - 11y + 46 = 0\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{235}}{{49}}\\y = \dfrac{{269}}{{49}}\end{array} \right.\).
Vậy \(T = \dfrac{{72}}{7}\).
Đường thẳng \(d:\dfrac{x}{a} + \dfrac{y}{b} = 1\), với $a \ne 0$, $b \ne 0$, đi qua điểm \(M\left( { - 1;6} \right)\) và tạo với các tia \(Ox\), \(Oy\) một tam giác có diện tích bằng \(4\). Tính $S = a + 2b$.
Đường thẳng \(d:\dfrac{x}{a} + \dfrac{y}{b} = 1\) đi qua điểm \(M\left( { - 1;6} \right)\) \( \Rightarrow \dfrac{{ - 1}}{a} + \dfrac{6}{b} = 1\left( 1 \right)\).
Gọi \(A,B\) lần lượt là giao điểm của \(d\) với các tia \(Ox,Oy\) thì \(A\left( {a;0} \right),B\left( {0;b} \right)\) và \(a,b > 0\).
Đường thẳng \(d:\dfrac{x}{a} + \dfrac{y}{b} = 1\) tạo với các tia \(Ox\);\(Oy\) tam giác có diện tích bằng \(4\)\( \Rightarrow ab = 8\left( 2 \right)\)
Từ $\left( 1 \right)$;$\left( 2 \right)$$ \Rightarrow \left\{ \begin{array}{l}\dfrac{{ - 1}}{a} + \dfrac{6}{b} = 1\\ab = 8\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{ - 1}}{a} + \dfrac{6}{b} = 1\\ab = 8\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{ - b}}{8} + \dfrac{6}{b} = 1\\ab = 8\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}b = 4\\a = 2\end{array} \right.$(nhận) hoặc$\left\{ \begin{array}{l}b = - 12\\a = - \dfrac{3}{2}\end{array} \right.$(Loại)
$ \Rightarrow a + 2b = 10$.
Đường thẳng \(\left( d \right)\) đi qua \(I\left( {3;2} \right)\) cắt \(Ox\); \(Oy\) tại $M$, $N$ sao cho $I$ là trung điểm của $MN$. Khi đó độ dài $MN$ bằng
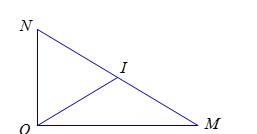
Dễ thấy tam giác $OMN$ vuông tại $O$ suy ra $MN = 2OI = 2\sqrt {{3^2} + {2^2}} = 2\sqrt {13} $.
Trong mặt phẳng tọa độ \(Oxy\), cho tam giác \(ABC\) có \(A\left( {3\,;\,4} \right)\), \(B\left( {2\,;\,1} \right)\), \(C\left( { - 1\,;\, - 2} \right)\). Gọi \(M\left( {x\,;\,y} \right)\) là điểm trên đường thẳng \(BC\) sao cho \({S_{\Delta ABC}} = 4{S_{\Delta ABM}}\). Tính \(P = x.y\).
Dễ thấy \(\dfrac{{{S_{\Delta ABC}}}}{{{S_{\Delta ABM}}}} = 4\)\( \Leftrightarrow \dfrac{{BC}}{{BM}} = 4\)\( \Leftrightarrow \left[ \begin{array}{l}\overrightarrow {BC} = 4\overrightarrow {BM} \\\overrightarrow {BC} = - 4\overrightarrow {BM} \end{array} \right.\).
TH1: \(\overrightarrow {BC} = 4\overrightarrow {BM} \) thì: \(\left\{ \begin{array}{l}x - 2 = - \dfrac{3}{4}\\y - 1 = - \dfrac{3}{4}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{5}{4}\\y = \dfrac{1}{4}\end{array} \right.\)\( \Rightarrow x.y = \dfrac{5}{{16}}\).
TH2: \(\overrightarrow {BC} = - 4\overrightarrow {BM} \) thì: \(\left\{ \begin{array}{l}x - 2 = \dfrac{3}{4}\\y - 1 = \dfrac{3}{4}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{11}}{4}\\y = \dfrac{7}{4}\end{array} \right.\)\( \Rightarrow x.y = \dfrac{{77}}{{16}}\).
Gọi \(H\) là trực tâm của tam giác \(ABC\). Phương trình các cạnh và đường cao của tam giác là \(AB\): \(7x - y + 4 = 0\); \(BH\): \(2x + y - 4 = 0\); \(AH\): \(x - y - 2 = 0\). Phương trình đường cao \(CH\) của tam giác \(ABC\) là
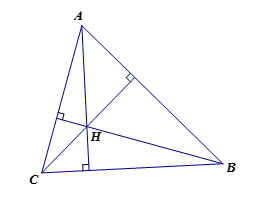
Gọi \(H\left( {x;y} \right)\).
Ta có \(H = AH \cap BH\).
Nên tọa độ điểm \(H\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}2x + y = 4\\x - y = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right.\), suy ra \(H\left( {2;0} \right)\).
Đường thẳng \(AB\) có vectơ chỉ phương là \(\overrightarrow u = \left( {1;7} \right)\).
Đường cao \(CH\) vuông góc với cạnh \(AB\) nên nhận \(\overrightarrow u \) làm vectơ pháp tuyến.
Vậy phương trình tổng quát của đường cao \(CH\) là \(\left( {x - 2} \right) + 7\left( {y - 0} \right) = 0\)\( \Leftrightarrow x + 7y - 2 = 0\).
Gọi \(\Delta \) là đường thẳng song song với đường thẳng \(d:3x - 2y + 12 = 0\) và cắt \(Ox\), \(Oy\) lần lượt tại \(A\), \(B\) sao cho \(AB = \sqrt {13} \). Phương trình nào dưới đây có thể là phương trình của \(\Delta \)?
Cách 1: Tự luận
Vì $\Delta \,{\rm{//}}\,d$ nên $\Delta $ có dạng $3x - 2y + c = 0$ với $c \ne 12$.
$\Delta $ cắt $Ox$, $Oy$ lần lượt tại $A$, $B$ suy ra tọa độ của $A\left( { - \dfrac{c}{3};0} \right)$ và $B\left( {0; - \dfrac{c}{2}} \right)$.
Theo đề bài $AB = \sqrt {13} \Leftrightarrow A{B^2} = 13 $ $\Leftrightarrow {\left( {\dfrac{c}{3}} \right)^2} + {\left( {\dfrac{c}{2}} \right)^2} = 13$ $ \Leftrightarrow {c^2} = 36 \Leftrightarrow c = \pm 6$
Với \(c = 6\): $\Delta :3x - 2y + 6 = 0$.
Với \(c = - 6\): $\Delta :3x - 2y - 6 = 0$ hay $\Delta :6x - 4y - 12 = 0$.

