Gọi \(H\) là trực tâm của tam giác \(ABC\). Phương trình các cạnh và đường cao của tam giác là \(AB\): \(7x - y + 4 = 0\); \(BH\): \(2x + y - 4 = 0\); \(AH\): \(x - y - 2 = 0\). Phương trình đường cao \(CH\) của tam giác \(ABC\) là

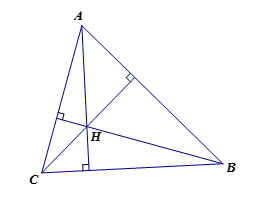
Gọi \(H\left( {x;y} \right)\).

Ta có \(H = AH \cap BH\).

Nên tọa độ điểm \(H\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}2x + y = 4\\x - y = 2\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 2\\y = 0\end{array} \right.\), suy ra \(H\left( {2;0} \right)\).

Đường thẳng \(AB\) có vectơ chỉ phương là \(\overrightarrow u  = \left( {1;7} \right)\).

Đường cao \(CH\) vuông góc với cạnh \(AB\) nên nhận \(\overrightarrow u \) làm vectơ pháp tuyến.

Vậy phương trình tổng quát của đường cao \(CH\) là \(\left( {x - 2} \right) + 7\left( {y - 0} \right) = 0\)\( \Leftrightarrow x + 7y - 2 = 0\).