Trong mặt phẳng tọa độ $Oxy$, cho tam giác $MNP$ vuông tại $M$. Biết điểm $M\left( {2;1} \right)$, $N\left( {3; - 2} \right)$ và \(P\) là điểm nằm trên trục $Oy$. Tính diện tích tam giác \(MNP\).
\(P\) nằm trên \(Oy\)\( \Rightarrow \) \(P\left( {0;\,p} \right)\) mà \(MNP\) vuông tại \(M\)\( \Rightarrow \)\(\overrightarrow {MP} .\overrightarrow {MN} = 0\).
Mà \(\overrightarrow {MP} = \left( { - 2;p - 1} \right),\overrightarrow {MN} = \left( {1; - 3} \right)\) nên \(\overrightarrow {MP} .\overrightarrow {MN} = 0 \) \(\Leftrightarrow - 2.1 + \left( {p - 1} \right).\left( { - 3} \right) = 0\)
\( \Leftrightarrow \) \( - 2 - 3p + 3 = 0\) \( \Leftrightarrow \)\(p = \dfrac{1}{3}\).
$ \Rightarrow P\left( {0;\dfrac{1}{3}} \right)$ $ \Rightarrow MP = \sqrt {{{\left( { - 2} \right)}^2} + {{\left( {\dfrac{1}{3} - 1} \right)}^2}}$ $ = \dfrac{{2\sqrt {10} }}{3}$, $MN = \sqrt {{1^2} + {{\left( { - 3} \right)}^2}} = \sqrt {10} $
\( \Rightarrow \)\(S = \dfrac{1}{2}\dfrac{{2\sqrt {10} }}{3}\sqrt {10} = \dfrac{{10}}{3}\).
Cho hai điểm \(P\left( {6;1} \right)\) và \(Q\left( { - 3; - 2} \right)\) và đường thẳng \(\Delta :2x - y - 1 = 0\). Tọa độ điểm \(M\) thuộc \(\Delta \) sao cho \(MP + MQ\) nhỏ nhất.
Đặt \(F\left( {x,y} \right) = 2x - y - 1\)
Thay \(P\left( {6;1} \right)\) vào \(F\left( {x;y} \right)\) \( \Rightarrow 2.6 - 1 - 1 = 10\)
Thay \(Q\left( { - 3; - 2} \right)\) vào \(F\left( {x;y} \right)\) \( \Rightarrow 2.\left( { - 3} \right) - \left( { - 2} \right) - 1 = - 5\).
Suy ra \(P,Q\) nằm về hai phía của đường thẳng \(\Delta \).
Ta có \(MP + MQ\) nhỏ nhất \( \Leftrightarrow M,P,Q\) thẳng hàng
\( \Leftrightarrow \overrightarrow {PQ} \) cùng phương \(\overrightarrow {PM} \).
Gọi \(M\left( {x;2x - 1} \right) \in \Delta \), khi đó \(\overrightarrow {PQ} = \left( { - 9; - 3} \right),\overrightarrow {PM} = \left( {x - 6;2x - 2} \right)\)
\(\overrightarrow {PQ} \) cùng phương \(\overrightarrow {PM} \)\( \Leftrightarrow \dfrac{{x - 6}}{{ - 9}} = \dfrac{{2x - 2}}{{ - 3}}\) \( \Leftrightarrow x = 0 \Rightarrow y = - 1\) \( \Rightarrow M\left( {0; - 1} \right)\)
Cho tam giác $ABC$ có $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và hai trong ba đường phân giác trong có phương trình lần lượt là $x - 2y - 1 = 0$, $x + 3y - 1 = 0$. Viết phương trình đường thẳng chứa cạnh $BC$.
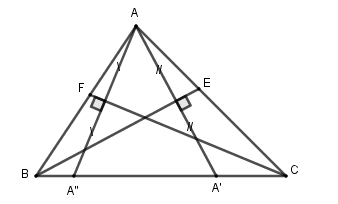
Dễ thấy điểm $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ không thuộc hai đường phân giác $x - 2y - 1 = 0$ và $x + 3y - 1 = 0$. Suy gọi $CF:x - 2y - 1 = 0$, $BE:x + 3y - 1 = 0$ lần lượt là phương trình đường phân giác xuất phát từ đỉnh $C$, $B$(như hình vẽ trên).
Gọi $d$ là đường thẳng qua $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và vuông góc với $BE$ thì $d$ có VTPT là $\overrightarrow {{n_d}} = \left( {3; - 1} \right)$ nên có phương trình $3\left( {x - \dfrac{4}{5}} \right) - \left( {y - \dfrac{7}{5}} \right) = 0 \Leftrightarrow $$3x - y - 1 = 0$. Tọa độ điểm $M = d \cap BE$ thỏa mãn hệ $\left\{ \begin{array}{l}3x - y - 1 = 0\\x + 3y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{5}\\y = \dfrac{1}{5}\end{array} \right. \Rightarrow $$M\left( {\dfrac{2}{5};\dfrac{1}{5}} \right)$.
Suy ra tọa độ điểm đối xứng với $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ qua $M\left( {\dfrac{2}{5};\dfrac{1}{5}} \right)$ là $A'\left( {0; - 1} \right)$ thì $A' \in BC$$\left( 1 \right)$.
Gọi $d'$ là đường thẳng qua $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ và vuông góc với $CF$ thì $d'$ có VTPT là $\overrightarrow {{n_{d'}}} = \left( {2;1} \right)$ nên có phương trình $2\left( {x - \dfrac{4}{5}} \right) + \left( {y - \dfrac{7}{5}} \right) = 0 \Leftrightarrow $$2x + y - 3 = 0$. Tọa độ điểm $N = d' \cap CF$ thỏa mãn hệ $\left\{ \begin{array}{l}2x + y - 3 = 0\\x - 2y - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{5}\\y = \dfrac{1}{5}\end{array} \right. \Rightarrow $$N\left( {\dfrac{7}{5};\dfrac{1}{5}} \right)$.
Suy ra tọa độ điểm đối xứng với $A\left( {\dfrac{4}{5};\dfrac{7}{5}} \right)$ qua $N\left( {\dfrac{7}{5};\dfrac{1}{5}} \right)$ là $A''\left( {2; - 1} \right)$ thì $A'' \in BC$$\left( 2 \right)$.
Từ $\left( 1 \right)$ và $\left( 2 \right)$ ta có $\overrightarrow {A'A''} = \left( {2;0} \right)$ là một VTCP của $BC$ suy ra VTPT của $BC$ là $\overrightarrow n = \left( {0;1} \right)$. Do đó phương trình cạnh $BC:0\left( {x - 0} \right) + 1\left( {y + 1} \right) = 0 \Leftrightarrow $ $y + 1 = 0$.
Cho hai đường thẳng \(d\) và \({d^\prime }\) biết \(d:2x + y - 8 = 0\) và \({d^\prime }:\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 3 - t}\end{array}} \right.\). Biết \(I\left( {a;{\rm{ }}b} \right)\) là tọa độ giao điểm của \(d\) và \({d^\prime }\). Khi đó tổng \(a + b\) bằng
Tham số \(t\) ứng với giao điểm của \(d\) và \({d^\prime }\) là nghiệm của phương trình
\(2\left( {1 + 2t} \right) + \left( {3 - t} \right) - 8 = 0\)\( \Leftrightarrow \)\(t = 1\). Khi đó \(\left\{ {\begin{array}{*{20}{l}}{x = 3}\\{y = 2}\end{array}} \right.\)\( \Rightarrow \)\(I\left( {3;{\rm{ }}2} \right)\)\( \Rightarrow \)\(a + b = 5\).
Trong mặt phẳng với hệ tọa độ \(Oxy\), cho điểm \(M\left( {1;2} \right)\) và đường thẳng \(d:2x + y - 5 = 0\). Toạ độ của điểm đối xứng với điểm \(M\) qua \(d\) là
Bước 1: Gọi M’ là điểm đối xứng của M qua d. Viết phương trình MM’.
\(\overrightarrow n = \left( {2;\,1} \right)\) là một VTPT của d
Gọi M’ là điểm đối xứng của M qua d \( \Rightarrow MM' \bot d\)
\( \Rightarrow \overrightarrow {{n_1}} = \left( { - 1;2} \right)\) là một VTPT của MM’
\( \Rightarrow \) Phương trình MM’: \( - 1\left( {x - 1} \right) + 2\left( {y - 2} \right) = 0 \Leftrightarrow - x + 2y - 3 = 0\)
Bước 2: Tìm điểm I là giao điểm của MM’ và d.
Gọi I là giao điểm của MM’ và d \( \Rightarrow \) Tọa độ điểm I là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l} - x + 2y - 3 = 0\\2x + y - 5 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{7}{5}\\y = \dfrac{{11}}{5}\end{array} \right.\) \( \Rightarrow I\left( {\dfrac{7}{5};\dfrac{{11}}{5}} \right) \Rightarrow \overrightarrow {MI} = \left( {\dfrac{2}{5};\dfrac{1}{5}} \right)\)
Gọi \(M'\left( {a;b} \right) \Rightarrow \overrightarrow {IM'} = \left( {a - \dfrac{7}{5};b - \dfrac{{11}}{5}} \right)\)
Bước 3: Từ \(\overrightarrow {MI} = \overrightarrow {IM'} \) để tìm M’.
Vì M’ là điểm đối xứng của M qua d \( \Rightarrow \) M’ là điểm đối xứng của M qua I
\( \Rightarrow \overrightarrow {MI} = \overrightarrow {IM'} \Rightarrow \left\{ \begin{array}{l}a - \dfrac{7}{5} = \dfrac{2}{5}\\b - \dfrac{{11}}{5} = \dfrac{1}{5}\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{9}{5}\\b = \dfrac{{12}}{5}\end{array} \right. \Rightarrow M'\left( {\dfrac{9}{5};\dfrac{{12}}{5}} \right)\)
Đường thẳng đi qua hai điểm A(-1;4) và B(2;-7) có phương trình là:
Gọi phương trình đường thẳng AB là y = ax + b.
Vì \(A \in AB\) nên 4 = –a + b.
Vì \(B \in AB\) nên –7 = 2a + b.
Ta có hệ phương trình
\(\left\{ \begin{array}{l} - a + b = 4\\2a + b = - 7\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \dfrac{{11}}{3}\\b = \dfrac{1}{3}\end{array} \right.\)
Vậy phương trình đường thẳng AB là \(y = - \dfrac{{11}}{3}x + \dfrac{1}{3}\) \( \Leftrightarrow 3y = - 11x + 1\)\( \Leftrightarrow 11x + 3y - 1 = 0\).
Đường thẳng đi qua \(A\left( { - 1;2} \right)\), nhận \(\overrightarrow n = \left( {2; - 4} \right)\) làm véc tơ pháp tuyến có phương trình là:
Gọi \(\left( d \right)\) là đường thẳng đi qua \(A\) và nhận \(\overrightarrow n = \left( {2; - 4} \right)\) hay \(\dfrac{1}{2}\overrightarrow n = \left( {1; - 2} \right)\) làm VTPT
\( \Rightarrow \left( d \right):x + 1 - 2\left( {y - 2} \right) = 0 \Leftrightarrow x - 2y + 5 = 0\)
Phương trình đường thẳng đi qua hai điểm \(A\left( { - 2;4} \right)\,;B\left( { - 6;1} \right)\) là:
Ta có: \(\overrightarrow {AB} = \left( { - 4; - 3} \right) \Rightarrow \overrightarrow {{n_{AB}}} = \left( {3; - 4} \right)\) là 1 VTPT của AB.
Đường thẳng AB đi qua A(-2;4) và nhận \(\overrightarrow {{n_{AB}}} = \left( {3; - 4} \right)\) làm VTPT nên có phương trình:
\(3\left( {x + 2} \right) - 4\left( {y - 4} \right) = 0\) hay \(3x - 4y + 22 = 0\).
Cho đường thẳng \(\left( d \right):3x + 5y - 15 = 0\). Phương trình nào sau đây không trùng (d).
Ta có đường thẳng \(\left( d \right):3x + 5y - 15 = 0\) có : \(\left\{ \begin{array}{l}\overrightarrow n = \left( {3;5} \right)\\A\left( {5;0} \right) \in d\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow u = \left( { - \dfrac{5}{3};1} \right)\\A\left( {5;0} \right) \in d\end{array} \right. \) \(\Rightarrow \left( d \right):\left\{ \begin{array}{l}x = 5 - \dfrac{5}{3}t\\y = t\end{array} \right.\)
Suy ra D đúng.
\(\left( d \right):3x + 5y - 15 = 0 \Leftrightarrow 3x + 5y = 15 \Leftrightarrow \dfrac{x}{5} + \dfrac{y}{3} = 1\)
Suy ra A đúng.
\(\left( d \right):3x + 5y - 15 = 0 \Leftrightarrow - 5y = 3x - 15 \Leftrightarrow y = - \dfrac{3}{5}x + 3\)
Suy ra B đúng.
Cho đường thẳng \(\left( d \right):x - 2y + 1 = 0\). Nếu đường thẳng \(\left( \Delta \right)\) đi qua \(M\left( {1; - 1} \right)\) và song song với \(\left( d \right)\) thì \(\left( \Delta \right)\) có phương trình
Ta có \(\left( \Delta \right)//\left( d \right)x - 2y + 1 = 0 \Rightarrow \left( \Delta \right):x - 2y + c = 0\left( {c \ne 1} \right)\)
Ta lại có \(M\left( {1; - 1} \right) \in \left( \Delta \right) \Rightarrow 1 - 2\left( { - 1} \right) + c = 0 \Leftrightarrow c = - 3\)
Vậy \(\left( \Delta \right):x - 2y - 3 = 0\)
Cho ba điểm \(A\left( {1; - 2} \right)\,,B\left( {5; - 4} \right)\,,C\left( { - 1;4} \right)\) . Đường cao \(AA'\) của tam giác $ABC$ có phương trình
Ta có \(\overrightarrow {BC} = \left( { - 6;8} \right)\)
Gọi \(AA'\) là đường cao của tam giác \(\Delta ABC\) \( \Rightarrow AA'\) nhận \(\left\{ \begin{array}{l}\overrightarrow n = \overrightarrow {BC} = \left( { - 6;8} \right)\\A\left( {1; - 2} \right)\end{array} \right.\)
Suy ra \(AA': - 6\left( {x - 1} \right) + 8\left( {y + 2} \right) = 0 \Leftrightarrow - 6x + 8y + 22 = 0 \Leftrightarrow 3x - 4y - 11 = 0\).
Trong mặt phẳng tọa độ \(Oxy\), cho hai điểm \(M\left( {6;{\rm{ }}3} \right)\), \(N\left( { - 3;{\rm{ 6}}} \right)\). Gọi \(P\left( {x;{\rm{ }}y} \right)\) là điểm trên trục hoành sao cho ba điểm \(M\), \(N\), \(P\) thẳng hàng, khi đó \(x + y\) có giá trị là
\(P\left( {x;{\rm{ }}y} \right)\) là điểm trên trục hoành nên suy ra \(P\left( {x;{\rm{ 0}}} \right)\).
Ta có: \(\overrightarrow {MN} = \left( { - 9;{\rm{ }}3} \right)\); \(\overrightarrow {MP} = \left( {x - 6;{\rm{ }} - 3} \right)\).
Ba điểm \(M\), \(N\), \(P\) thẳng hàng khi \(\overrightarrow {MP} = k\overrightarrow {MN} \)\( \Leftrightarrow \)\(\left\{ \begin{array}{l}x - 6 = k.\left( { - 9} \right)\\ - 3 = k.3\end{array} \right.\) \( \Leftrightarrow \)\(\left\{ \begin{array}{l}x = 15\\k = - 1\end{array} \right.\).
Vậy \(P\left( {15;{\rm{ 0}}} \right)\), suy ra \(x + y = 15\).
Cho đường thẳng \(\left( d \right):4x - 3y + 5 = 0\). Nếu đường thẳng \(\left( \Delta \right)\) đi qua góc tọa độ và vuông góc với \(\left( d \right)\) thì \(\left( \Delta \right)\)có phương trình:
Ta có: \(\overrightarrow {{n_d}} = \left( {4; - 3} \right) \Rightarrow \overrightarrow {{u_d}} = \left( {3;4} \right)\)
Đường thẳng \(\Delta \bot d \Rightarrow \Delta \) nhận \(\overrightarrow {{u_d}} = \left( {3;4} \right)\) làm VTPT và đi qua \(O\left( {0;0} \right)\).
Khi đó: \(\left( \Delta \right):3\left( {x - 0} \right) + 4\left( {y - 0} \right) = 0\) hay $3x+4y=0$
Cho hai điểm \(A\left( { - 2;3} \right)\,;B\left( {4; - 1} \right).\) Viết phương trình trung trực đoạn AB.
Gọi \(M\) trung điểm \(AB\) \( \Rightarrow M\left( {1;1} \right)\)
Ta có \(\overrightarrow {AB} = \left( {6; - 4} \right)\)
Gọi \(d\) là đường thẳng trung trực của \(AB\).
Phương trình \(d\) nhận \(\overrightarrow n = \left( {6; - 4} \right)\) làm VTPT và đi qua \(M\left( {1;1} \right)\)
Suy ra \(\left( d \right):6\left( {x - 1} \right) - 4\left( {y - 1} \right) = 0 \Leftrightarrow 6x - 4y - 2 = 0 \Leftrightarrow 3x - 2y - 1 = 0\)
Cho tam giác \(ABC\) có \(A\left( { - 1; - 2} \right);B\left( {0;2} \right);C\left( { - 2;1} \right)\). Đường trung tuyến \(BM\) có phương trình là:
Gọi \(M\) là trung điểm \(AC\) \( \Rightarrow M\left( { - \dfrac{3}{2}; - \dfrac{1}{2}} \right)\) . \(\overrightarrow {BM} = \left( { - \dfrac{3}{2}; - \dfrac{5}{2}} \right)\)
\(BM\) qua \(B\left( {0;2} \right)\) và nhận \(\overrightarrow n = \left( {5; - 3} \right)\) làm VTPT \( \Rightarrow BM:5x - 3\left( {y - 2} \right) = 0 \Leftrightarrow 5x - 3y + 6 = 0\)
Phương trình tham số của đường thẳng đi qua điểm \(A\left( {2;\, - 1} \right)\) và nhận \(\overrightarrow u = \left( { - 3;\,2} \right)\) làm vectơ chỉ phương là
Phương trình tham số của đường thẳng đi qua điểm \(A\left( {2;\, - 1} \right)\) và nhận \(\overrightarrow u = \left( { - 3;\,2} \right)\) làm vectơ chỉ phương có dạng: \(\left\{ \begin{array}{l}x = 2 - 3t\\y = - 1 + 2t\end{array} \right.\)
Cho \(\left( d \right):\left\{ \begin{array}{l}x = 2 + 3t\\y = 3 + t.\end{array} \right.\) . Hỏi có bao nhiêu điểm \(M \in \left( d \right)\) cách \(A\left( {9;1} \right)\) một đoạn bằng $5.$
Gọi $M\left( {2 + 3m;3 + m} \right)$ \( \Rightarrow AM = \sqrt {{{\left( {2 + 3m - 9} \right)}^2} + {{\left( {3 + m - 1} \right)}^2}} \) \( = \sqrt {10{m^2} - 38m + 53} \)
Theo YCBT ta có $AM = 5 \Leftrightarrow A{M^2} = 25$$ \Leftrightarrow 10{m^2} - 38m + 53 = 25$ $ \Leftrightarrow 10{m^2} - 38m + 28 = 0$\( \Leftrightarrow \left[ \begin{array}{l}m = 1 \Rightarrow M\left( {5;4} \right)\\m = \dfrac{{14}}{5} \Rightarrow M\left( {\dfrac{{52}}{5};\dfrac{{29}}{5}} \right)\end{array} \right.\)
Vậy có hai điểm $M$ thỏa YCBT.
Cho tam giác \(ABC\) biết trực tâm \(H\left( {1;\;1} \right)\) và phương trình cạnh \(AB:5x - 2y + 6 = 0\), phương trình cạnh \(AC:4x + 7y - 21 = 0\). Phương trình cạnh \(BC\) là
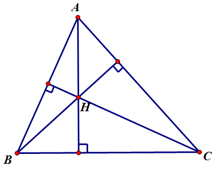
Phương trình \(AB:5x - 2y + 6 = 0\)\( \Rightarrow \overrightarrow {{n_{AB}}} = \left( {5;\; - 2} \right)\).
Phương trình \(AC:4x + 7y - 21 = 0\)\( \Rightarrow \overrightarrow {{n_{AC}}} = \left( {4;\;7} \right)\).
Ta có \(BH \bot AC\)\( \Rightarrow \overrightarrow {{n_{BH}}} .\overrightarrow {{n_{AC}}} = 0 \Rightarrow \overrightarrow {{n_{BH}}} = \left( {7;\; - 4} \right)\).
Suy ra phương trình đường thẳng \(BH\) có \(\left\{ \begin{array}{l}\overrightarrow {{n_{BH}}} = \left( {7; - 4} \right)\\H\left( {1;1} \right)\end{array} \right.\).
\(BH:7\left( {x - 1} \right) - 4\left( {y - 1} \right) = 0 \Leftrightarrow 7x - 4y - 3 = 0\).
Ta có điểm \(B\) là giao điểm của hai đường thẳng \(AB\) và \(BH\), suy ra tọa độ điểm \(B\) là nghiệm của hệ phương trình \(\left\{ \begin{array}{l}5x - 2y + 6 = 0\\7x - 4y - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 5\\y = - \dfrac{{19}}{2}\end{array} \right.\) \( \Rightarrow B\left( { - 5;\; - \dfrac{{19}}{2}} \right)\).
\(A\) là giao điểm của \(AB,AC\) thì \(\left\{ \begin{array}{l}5x - 2y + 6 = 0\\4x + 7y - 21 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x = 0\\y = 3\end{array} \right. \Rightarrow A\left( {0;3} \right)\).
Phương trình cạnh \(BC\) có \(\left\{ \begin{array}{l}\overrightarrow {{n_{BC}}} = \overrightarrow {AH} = \left( {1; - 2} \right)\\B\left( { - 5; - \dfrac{{19}}{2}} \right)\end{array} \right.\).
\( \Rightarrow BC:x + 5 - 2\left( {y + \dfrac{{19}}{2}} \right) = 0\) \( \Leftrightarrow x - 2y - 14 = 0\)
Vậy \(BC:x - 2y - 14 = 0\).
Cho 4 điểm \(A\left( { - 3;1} \right),B\left( { - 9; - 3} \right),C\left( { - 6;0} \right),D\left( { - 2;4} \right)\). Tìm tọa độ giao điểm của 2 đường thẳng \(AB\) và \(CD\).
Ta có \(\overrightarrow {AB} = \left( { - 6; - 4} \right)\)\( \Rightarrow \overrightarrow {{n_{AB}}} = \left( {2; - 3} \right) \)
Đường thẳng $AB$ qua $A(-3;1)$ và nhận \(\overrightarrow {{n_{AB}}} = \left( {2; - 3} \right) \) làm vecto pháp tuyến có phương trình là: $2.(x+3)-3(y-1)=0$
\(\Rightarrow \left( {AB} \right):2x - 3y = - 9\)
Ta có \(\overrightarrow {CD} = \left( {4;4} \right) \Rightarrow \overrightarrow {{n_{CD}}} = \left( {1; - 1} \right) \Rightarrow \left( {CD} \right):x - y = - 6\)
Gọi \(N = AB \cap CD\)
Suy ra tọa độ của \(N\) là nghiệm của hệ \(\left\{ \begin{array}{l}2x - 3y = - 9\\x - y = - 6\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = - 9\\y = - 3\end{array} \right. \Rightarrow N\left( { - 9; - 3} \right)\)
Cho tam giác \(ABC\) với \(A\left( {2;3} \right);B\left( { - 4;5} \right);C\left( {6; - 5} \right)\). \(M,N\) lần lượt là trung điểm của \(AB\) và \(AC\). Phương trình tham số của đường trung bình \(MN\) là:
Ta có: \(M\left( { - 1;4} \right);N\left( {4; - 1} \right)\).
\(MN\) đi qua \(M\left( { - 1;4} \right)\) và nhận \(\overrightarrow {MN} = \left( {5; - 5} \right)\) hay $\dfrac{1}{5}\overrightarrow {MN} = \left( {1; - 1} \right)$ làm \(VTCP\)
\( \Rightarrow MN:\left\{ \begin{array}{l}x = - 1 + t\\y = 4 - t\end{array} \right.\)

