Cho tam giác \(ABC\) có \(\widehat B = {30^0},\widehat C = {105^0}\) và \(AC = 6\). Kết quả nào trong các kết quả sau là độ dài của cạnh \(BC\)?
+ Có \(\widehat A = {180^0} - {30^0} - {105^0} = {45^0}\)
+ \(\dfrac{b}{{\sin B}} = \dfrac{a}{{\sin A}} \Rightarrow a = \dfrac{b}{{\sin B}}.\sin A = \dfrac{6}{{\sin {{30}^0}}}.\sin {45^0} = 6\sqrt 2 .\)
Tam giác \(ABC\) có \(AB = 2,\;AC = 1\) và \(\widehat A = 60^\circ \). Tính độ dài cạnh \(BC\).
Theo định lí hàm cosin, ta có
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat A = {2^2} + {1^2} - 2.2.1.\cos 60^\circ = 3 \Rightarrow BC = \sqrt 3 \).
Tam giác \(ABC\) có \(AB = \sqrt 2 ,\;AC = \sqrt 3 \) và \(\widehat C = 45^\circ \). Tính độ dài cạnh \(BC\).
Theo định lí hàm cosin, ta có
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat C\)\( \Rightarrow {\left( {\sqrt 2 } \right)^2} = {\left( {\sqrt 3 } \right)^2} + B{C^2} - 2.\sqrt 3 .BC.\cos 45^\circ \)
\( \Rightarrow BC = \dfrac{{\sqrt 6 + \sqrt 2 }}{2}\).
Tam giác \(ABC\) có \(AB = 4,\;BC = 6,\;AC = 2\sqrt 7 \). Điểm \(M\) thuộc đoạn \(BC\) sao cho \(MC = 2MB\). Tính độ dài cạnh \(AM\).
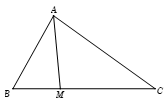
Theo định lí hàm cosin, ta có : \(\cos B = \dfrac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}}\) \( = \dfrac{{{4^2} + {6^2} - {{\left( {2\sqrt 7 } \right)}^2}}}{{2.4.6}} = \dfrac{1}{2}\).
Do \(MC = 2MB \Rightarrow BM = \dfrac{1}{3}BC = 2\).
Theo định lí hàm cosin, ta có
\(A{M^2} = A{B^2} + B{M^2} - 2.AB.BM.\cos \widehat B\)\( = {4^2} + {2^2} - 2.4.2.\dfrac{1}{2} = 12\)
\( \Rightarrow AM = 2\sqrt 3 \)
Tam giác \(ABC\) vuông tại \(A\) và có \(AB = AC = a\). Tính độ dài đường trung tuyến \(BM\) của tam giác đã cho
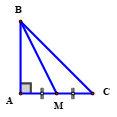
\(M\) là trung điểm của \(AC \Rightarrow AM = \dfrac{{AC}}{2} = \dfrac{a}{2}.\)
Tam giác \(\Delta BAM\) vuông tại \(A\)
\( \Rightarrow BM = \sqrt {A{B^2} + A{M^2}} = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}.\)
Tam giác \(ABC\) có \(AB = 9\)cm, \(AC = 12\)cm và \(BC = 15\)cm. Tính độ dài đường trung tuyến \(AM\) của tam giác đã cho
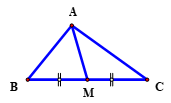
Áp dụng hệ thức đường trung tuyến \(m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\) ta được:
\(m_a^2 = \dfrac{{A{C^2} + A{B^2}}}{2} - \dfrac{{B{C^2}}}{4} = \dfrac{{{{12}^2} + {9^2}}}{2} - \dfrac{{{{15}^2}}}{4} = \dfrac{{225}}{4}.\)
\( \Rightarrow {m_a} = \dfrac{{15}}{2}.\)
Tam giác \(ABC\) có \(a = 21,{\rm{ }}b = 17,{\rm{ }}c = 10\). Diện tích của tam giác \(ABC\) bằng
Ta có \(p = \dfrac{{21 + 17 + 10}}{2} = 24\).
Do đó \(S = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \) \( = \sqrt {24\left( {24 - 21} \right)\left( {24 - 17} \right)\left( {24 - 10} \right)} = 84\).
Tam giác \(ABC\) có \(BC = a,CA = b,AB = c\) và có diện tích \(S\) . Nếu tăng cạnh \(BC\) lên \(2\) lần đồng thời tăng cạnh \(CA\) lên \(2\) lần và giữ nguyên độ lớn của góc \(C\) thì khi đó diện tích tam giác mới được tạo nên bằng:
+ Có \(S = \dfrac{1}{2}BC.CA.\sin C\)
+ Gọi \(S'\) là diện tích tam giác khi tăng cạnh \(BC\) lên \(2\) lần đồng thời tăng cạnh \(CA\) lên \(2\) lần và giữ nguyên độ lớn của góc \(C\) , ta có: \(S' = \dfrac{1}{2}.2BC.2CA.\sin C = 4S\)
Tam giác \(ABC\) có \(AB = 3,{\rm{ }}AC = 6\) và \(\widehat A = 60^\circ \). Tính bán kính \(R\) của đường tròn ngoại tiếp tam giác \(ABC\).
Áp dụng định lí Cosin, ta có \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos \widehat {BAC}\)
\( = {3^2} + {6^2} - 2.3.6.cos{60^0} = 27\)\( \Rightarrow B{C^2} = 27\)
\( \Rightarrow B{C^2} + A{B^2} = A{C^2}\)
Suy ra tam giác \(ABC\) vuông tại \(B,\) do đó bán kính \(R = \dfrac{{AC}}{2} = 3.\)
Sau 3 giờ tàu thứ nhất đi được quãng đường :\(AB = 20.3 = 60\;\;\left( {km} \right)\)
Sau 3 giờ tàu thứ hai đi được quãng đường : \(AC = 30.3 = 90\;\;\left( {km} \right)\)
Sau 3 giờ khoảng cách giữa hai tàu là :
\(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.\cos \angle A} = \sqrt {{{60}^2} + {{90}^2} - 2.60.90.\cos {{60}^o}} = 30\sqrt 7 \;\left( {km} \right)\)
Tam giác \(ABC\) cân tại \(C\), có \(AB = 9{\rm{cm}}\) và \(AC = \dfrac{{15}}{2}{\rm{cm}}\). Gọi \(D\) là điểm đối xứng của \(B\) qua \(C\). Tính độ dài cạnh \(AD.\)
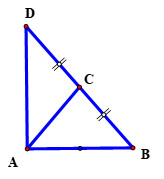
Ta có: \(D\) là điểm đối xứng của \(B\) qua \(C\)\( \Rightarrow C\) là trung điểm của \(BD.\)
\( \Rightarrow \) \(AC\) là trung tuyến của tam giác \(\Delta DAB.\)
\(BD = 2BC = 2AC = 15.\)
Theo hệ thức trung tuyến ta có:
\(A{C^2} = \dfrac{{A{B^2} + A{D^2}}}{2} - \dfrac{{B{D^2}}}{4}\) \( \Rightarrow A{D^2} = 2A{C^2} + \dfrac{{B{D^2}}}{2} - A{B^2}\)
\( \Rightarrow A{D^2} = \) \(2.{\left( {\dfrac{{15}}{2}} \right)^2} + \dfrac{{{{15}^2}}}{2} - {9^2} = 144 \Rightarrow AD = 12.\)
Tam giác \(ABC\) có \(AB = c,\;BC = a,\;CA = b\). Các cạnh \(a,\;b,\;c\) liên hệ với nhau bởi đẳng thức \(b\left( {{b^2} - {a^2}} \right) = c\left( {{a^2} - {c^2}} \right)\). Khi đó góc \(\widehat {BAC}\) bằng bao nhiêu độ?
Theo định lí hàm cosin, ta có \(\cos \widehat {BAC} = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}}\)\( = \dfrac{{{c^2} + {b^2} - {a^2}}}{{2bc}}\)
Mà \(b\left( {{b^2} - {a^2}} \right) = c\left( {{a^2} - {c^2}} \right)\)\( \Leftrightarrow {b^3} - {a^2}b = {a^2}c - {c^3}\) \( \Leftrightarrow - {a^2}\left( {b + c} \right) + \left( {{b^3} + {c^3}} \right) = 0\)
\( \Leftrightarrow \left( {b + c} \right)\left( {{b^2} + {c^2} - {a^2} - bc} \right) = 0\)\( \Leftrightarrow {b^2} + {c^2} - {a^2} - bc = 0\) (do \(b > 0,\;c > 0\))
\( \Leftrightarrow {b^2} + {c^2} - {a^2} = bc\)
Khi đó, \(\cos \widehat {BAC} = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \dfrac{1}{2}\)\( \Rightarrow \widehat {BAC} = 60^\circ \)
Theo định lý hàm số sin ta có : \(\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow \) đáp án A sai.
Hình bình hành \(ABCD\) có \(AB = a,{\rm{ }}BC = a\sqrt 2 \) và \(\widehat {BAD} = {45^0}\). Khi đó hình bình hành có diện tích bằng
Diện tích tam giác \(ABD\) là \({S_{\Delta ABD}} = \dfrac{1}{2}.AB.AD.\sin \widehat {BAD}\)\( = \dfrac{1}{2}.a.a\sqrt 2 .\sin {45^0} = \dfrac{{{a^2}}}{2}\)
Vậy diện tích hình bình hành \(ABCD\) là \({S_{ABCD}} = 2.{S_{\Delta ABD}} = 2.\dfrac{{{a^2}}}{2} = {a^2}.\)
Tam giác \(ABC\) có \(AB = 5,\;BC = 7,\;CA = 8\). Số đo góc \(\widehat A\) bằng:
Theo định lí hàm cosin, ta có \(\cos \widehat A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2AB.AC}}\)\( = \dfrac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \dfrac{1}{2}\)
Do đó, \(\widehat A = 60^\circ \).
Ta có: \(p = \dfrac{{BC + AC + AB}}{2}\)\( = \dfrac{{9 + 11 + 8}}{2} = 14.\)
\( \Rightarrow {S_{ABC}} \)\(= \sqrt {14\left( {14 - 9} \right)\left( {14 - 11} \right)\left( {14 - 8} \right)} \)\(= 6\sqrt {35} \)
Tam giác \(ABC\) vuông tại \(A\) có \(AB = 6\)cm, \(BC = 10\)cm. Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho.
Dùng Pitago tính được \(AC = 8\), suy ra \(p = \dfrac{{AB + BC + CA}}{2} = 12\).
Diện tích tam giác vuông \(S = \dfrac{1}{2}AB.AC = 24\).
Lại có \(S = p.r \Rightarrow r = \dfrac{S}{p} = 2{\rm{cm}}{\rm{.}}\)
Tam giác \(ABC\) có \(AB = 5,{\rm{ }}AC = 8\) và \(\widehat {BAC} = {60^0}\). Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho.
Áp dụng định lý hàm số côsin, ta có
\(B{C^2} = A{B^2} + A{C^2} - 2AB.AC\cos A = 49\)\( \Rightarrow BC = 7\)
Diện tích \(S = \dfrac{1}{2}AB.AC.\sin A\)\( = \dfrac{1}{2}.5.8.\dfrac{{\sqrt 3 }}{2} = 10\sqrt 3 \)
Lại có \(S = p.r\)\( \Rightarrow r = \dfrac{S}{p} = \dfrac{{2S}}{{AB + BC + CA}} = \sqrt 3 \).
Tam giác \(ABC\) có \(a = 21,{\rm{ }}b = 17,{\rm{ }}c = 10\). Tính bán kính \(r\) của đường tròn nội tiếp tam giác đã cho.
Ta có \(p = \dfrac{{21 + 17 + 10}}{2} = 24\).
Suy ra \(S = \sqrt {24\left( {24 - 21} \right)\left( {24 - 17} \right)\left( {24 - 10} \right)} = 84\).
Lại có \(S = p.r \Rightarrow r = \dfrac{S}{p} = \dfrac{{84}}{{24}} = \dfrac{7}{2}.\)
Tính bán kính \(r\) của đường tròn nội tiếp tam giác đều cạnh \(a\).
Diện tích tam giác đều cạnh \(a\) bằng: \(S = \dfrac{1}{2}a.a.\sin {60^0} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Lại có \(S = pr\)\( \Rightarrow r = \dfrac{S}{p} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{4}}}{{\dfrac{{3a}}{2}}} = \dfrac{{a\sqrt 3 }}{6}\)

