Câu hỏi:
3 năm trước
Tam giác \(ABC\) cân tại \(C\), có \(AB = 9{\rm{cm}}\) và \(AC = \dfrac{{15}}{2}{\rm{cm}}\). Gọi \(D\) là điểm đối xứng của \(B\) qua \(C\). Tính độ dài cạnh \(AD.\)
Trả lời bởi giáo viên
Đáp án đúng: c
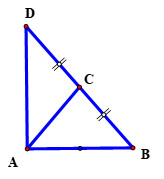
Ta có: \(D\) là điểm đối xứng của \(B\) qua \(C\)\( \Rightarrow C\) là trung điểm của \(BD.\)
\( \Rightarrow \) \(AC\) là trung tuyến của tam giác \(\Delta DAB.\)
\(BD = 2BC = 2AC = 15.\)
Theo hệ thức trung tuyến ta có:
\(A{C^2} = \dfrac{{A{B^2} + A{D^2}}}{2} - \dfrac{{B{D^2}}}{4}\) \( \Rightarrow A{D^2} = 2A{C^2} + \dfrac{{B{D^2}}}{2} - A{B^2}\)
\( \Rightarrow A{D^2} = \) \(2.{\left( {\dfrac{{15}}{2}} \right)^2} + \dfrac{{{{15}^2}}}{2} - {9^2} = 144 \Rightarrow AD = 12.\)
Hướng dẫn giải:
Sử dụng công thức trung tuyến đối với tam giác \(ABD\) để tính \(AD\).

