Tam giác \(ABC\) có ba đường trung tuyến \({m_a},{\rm{ }}{m_b},{\rm{ }}{m_c}\) thỏa mãn \(5m_a^2 = m_b^2 + m_c^2\). Khi đó tam giác này là tam giác gì?
Ta có: \(\left\{ \begin{array}{l}m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\\m_b^2 = \dfrac{{{a^2} + {c^2}}}{2} - \dfrac{{{b^2}}}{4}\\m_c^2 = \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}\end{array} \right.\)
Mà: \(5m_a^2 = m_b^2 + m_c^2\)
\( \Rightarrow 5\left( {\dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}} \right)\) \( = \dfrac{{{a^2} + {c^2}}}{2} - \dfrac{{{b^2}}}{4} + \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}\)
$\Leftrightarrow 5\left( {\dfrac{{{2b^2} + {2c^2}-a^2}}{4}} \right)$$=\dfrac{2{a^2} + 2{c^2} - {b^2} + 2{a^2} + 2{b^2} - {c^2}}{4}$
$\Leftrightarrow 5\left( {{2b^2} + {2c^2}-a^2} \right)$$=2{a^2} + 2{c^2} - {b^2} + 2{a^2} + 2{b^2} - {c^2}$
\( \Leftrightarrow 10{b^2} + 10{c^2} - 5{a^2} \)\(= 2{a^2} + 2{c^2} - {b^2} + 2{a^2} + 2{b^2} - {c^2}\)
\( \Leftrightarrow {b^2} + {c^2} = {a^2} \Rightarrow \) tam giác \(\Delta ABC\) vuông.
Tam giác \(ABC\) có \(AB = c,{\rm{ }}BC = a,{\rm{ }}CA = b\). Gọi \({m_a},{\rm{ }}{m_b},{\rm{ }}{m_c}\) là độ dài ba đường trung tuyến, \(G\) trọng tâm. Xét các khẳng định sau:
\(\left( {\rm{I}} \right)\). \(m_a^2 + m_b^2 + m_c^2 = \dfrac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right)\). \(\left( {{\rm{II}}} \right)\). \(G{A^2} + G{B^2} + G{C^2} = \dfrac{1}{3}\left( {{a^2} + {b^2} + {c^2}} \right)\).
Trong các khẳng định đã cho có
Mệnh đề \(\left( I \right)\): \(\left\{ \begin{array}{l}m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\\m_b^2 = \dfrac{{{a^2} + {c^2}}}{2} - \dfrac{{{b^2}}}{4}\\m_c^2 = \dfrac{{{a^2} + {b^2}}}{2} - \dfrac{{{c^2}}}{4}\end{array} \right.\)\( \Rightarrow m_a^2 + m_b^2 + m_c^2 = \dfrac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right)\)
Mệnh đề \(\left( {II} \right)\):\(G{A^2} + G{B^2} + G{C^2}\)\( = \dfrac{4}{9}\left( {m_a^2 + m_b^2 + m_c^2} \right)\) \( = \dfrac{4}{9}.\dfrac{3}{4}\left( {{a^2} + {b^2} + {c^2}} \right)\) \( = \dfrac{1}{3}\left( {{a^2} + {b^2} + {c^2}} \right)\).
Cho góc \(\widehat {xOy} = 30^\circ \). Gọi \(A\) và \(B\) là hai điểm di động lần lượt trên \(Ox\) và \(Oy\) sao cho \(AB = 1\). Khi \(OB\) có độ dài lớn nhất thì độ dài của đoạn \(OA\) bằng:
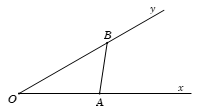
Theo định lí hàm sin, ta có
\(\dfrac{{OB}}{{\sin \widehat {OAB}}} = \dfrac{{AB}}{{\sin \widehat {AOB}}}\)\( \Leftrightarrow OB = \dfrac{{AB}}{{\sin \widehat {AOB}}}.\sin \widehat {OAB}\) \( = \dfrac{1}{{\sin 30^\circ }}.\sin \widehat {OAB} = 2\sin \widehat {OAB}\)
Do đó, độ dài \(OB\) lớn nhất khi và chỉ khi \(\sin \widehat {OAB} = 1 \Leftrightarrow \widehat {OAB} = 90^\circ \).
Khi đó \(OB = 2\).
Tam giác \(OAB\) vuông tại \(A\)\( \Rightarrow OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \)
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng \(CD = 60{\rm{m}}\), giả sử chiều cao của giác kế là \(OC = 1{\rm{m}}\). Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh \(A\) của tháp. Đọc trên giác kế số đo của góc \(\widehat {AOB} = {60^0}\). Chiều cao của ngọn tháp gần với giá trị nào sau đây:
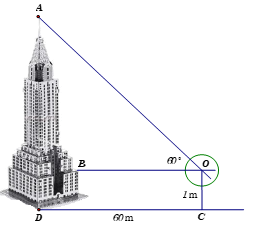
Tam giác \(OAB\) vuông tại \(B,\) có \(\tan \widehat {AOB} = \dfrac{{AB}}{{OB}} \Rightarrow AB = \tan {60^0}.OB = 60\sqrt 3 m.\)
Vậy chiều cao của ngọn tháp là \(h = AB + OC = \left( {60\sqrt 3 + 1} \right)\,{\rm{m}}.\)
. Giả sử \(CD = h\) là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,{\rm{ }}B\) trên mặt đất sao cho ba điểm \(A,{\rm{ }}B\) và \(C\) thẳng hàng. Ta đo được \(AB = 24{\rm{ m}}\), \(\widehat {CAD} = {63^0},{\rm{ }}\widehat {CBD} = {48^0}\).
Chiều cao \(h\) của tháp gần với giá trị nào sau đây?
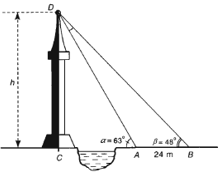
Áp dụng định lí sin vào tam giác \(ABD,\) ta có \(\dfrac{{AD}}{{\sin \beta }} = \dfrac{{AB}}{{\sin D}}.\)
Ta có \(\alpha = \widehat D + \beta \) nên \(\widehat D = \alpha - \beta = {63^0} - {48^0} = {15^0}.\)
Do đó \(AD = \dfrac{{AB.\sin \beta }}{{\sin \left( {\alpha - \beta } \right)}} = \dfrac{{24.\sin {{48}^0}}}{{\sin {{15}^0}}} \approx 68,91{\rm{ m}}.\)
Trong tam giác vuông \(ACD,\) có \(h = CD = AD.\sin \alpha \approx 61,4{\rm{ m}}.\)
Cho tam giác \(ABC\) có \(AB = 5,BC = 7,CA = 8.\) Số đo góc \(A\) bằng
Áp dụng định lý hàm số cos cho \(\Delta ABC\) ta có:
\(\begin{array}{l}\cos A = \dfrac{{A{B^2} + A{C^2} - B{C^2}}}{{2.AB.AC}} = \dfrac{{{5^2} + {8^2} - {7^2}}}{{2.5.8}} = \dfrac{1}{2}\\ \Rightarrow \angle A = {60^0}.\end{array}\)
Trong tam giác \(ABC\) có:
Ta có: ${a^2} = {b^2} + {c^2} - 2bc\cos A$
Trong tam giác\(ABC\) có
Ta có: \(\dfrac{a}{{\sin \,A}} = \dfrac{b}{{\sin \,B}} = \dfrac{c}{{\sin \,C}} = 2R \Rightarrow a = 2R\sin A.\)
Trong tam giác $ABC$ có
Trong tam giác $ABC$, độ dài trung tuyến kẻ từ đỉnh $A$ là \(m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\)
Trong tam giác $ABC$ ta có:
Ta có: \(\dfrac{a}{{\sin \,A}} = \dfrac{b}{{\sin \,B}} = \dfrac{c}{{\sin \,C}} = 2R \Rightarrow a\sin B = b\sin A.\)
Trong tam giác $ABC$, ta có.
Ta có \(\dfrac{1}{2}a.{h_a} = \dfrac{{abc}}{{4R}}\). Suy ra \({h_a} = \dfrac{{bc}}{{2R}}.\) hay \(bc = 2R.{h_a}\).
Trong tam giác $ABC$, tìm hệ thức sai.
+ ) \(\dfrac{1}{2}a.{h_a} = \dfrac{1}{2}ab.\sin C = \dfrac{1}{2}ac.\sin B\)
Suy ra \({h_a} = b.\sin C = c.\sin B\). Suy ra mệnh đề đáp án A và B đúng.
+ ) \(\dfrac{1}{2}c.{h_c} = \dfrac{1}{2}ab.\sin C\). Suy ra \(c.{h_c} = ab.\sin C\). Suy ra mệnh đề đáp án D đúng.
Cho tam giác $ABC$ có \(\widehat B = {60^0},\widehat C = {45^0}\) và $AB = 5$. Kết quả nào trong các kết quả sau là độ dài của cạnh $AC$?
\(\dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}} \Rightarrow b = \dfrac{c}{{\sin C}}.\sin B = \dfrac{5}{{\sin {{45}^0}}}.\sin {60^0} = \dfrac{{5\sqrt 6 }}{2}.\)
Cho tam giác $ABC$ có $b = 10,c = 16$ và góc \(\widehat A = {60^0}\). Kết quả nào trong các kết quả sau là độ dài của cạnh $BC$?
$\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\ = {10^2} + {16^2} - 2.10.16.\cos {60^0}\\ = {\rm{ }}196\end{array}$ .
Suy ra \(BC = a = \sqrt {196} = 14\).
Tam giác \(ABC\) có đoạn thẳng nối trung điểm của \(AB\) và \(BC\) bằng \(3\), cạnh \(AB = 9\) và \(\widehat {ACB} = 60^\circ \). Tính độ dài cạnh cạnh \(BC\).
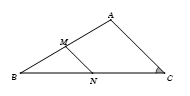
Bước 1: Tính \(AC\)
Gọi \(M,\;N\) lần lượt là trung điểm của \(AB,\;BC\).
\( \Rightarrow MN\) là đường trung bình của \(\Delta ABC\).
\( \Rightarrow MN = \dfrac{1}{2}AC\). Mà \(MN = 3\), suy ra \(AC = 6\).
Bước 2: Sử dụng định lý cô sin cho tam giác \(ABC\)
Theo định lí hàm cosin, ta có
\(\begin{array}{l}A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}\\ \Leftrightarrow {9^2} = {6^2} + B{C^2} - 2.6.BC.\cos 60^\circ \\ \Rightarrow BC = 3 + 3\sqrt 6 \end{array}\)
Cho tam giác $ABC$ có $a = 10,b = 6$ và $c = 8$. Kết quả nào trong các kết quả sau là số đo độ dài của trung tuyến $AM$?
\(m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4} = \dfrac{{{6^2} + {8^2}}}{2} - \dfrac{{{{10}^2}}}{4} = 25 \Rightarrow {m_a} = 5.\)
Tam giác $ABC$ có ba cạnh là $5,12,13$. Khi đó, diện tích tam giác là:
+ Ta có \(p = \dfrac{{a + b + c}}{2} = \dfrac{{5 + 12 + 13}}{2} = 15\)
+ \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15.10.3.2} = \sqrt {900} = 30\)
Tam giác $ABC$ có $BC = a,CA = b,AB = c$ và có diện tích $S$ . Nếu tăng cạnh $BC$ lên $2$ lần đồng thời tăng cạnh $CA$ lên $3$ lần và giữ nguyên độ lớn của góc $C$ thì khi đó diện tích tam giác mới được tạo nên bằng:
+ Có \(S = \dfrac{1}{2}BC.CA.\sin C\)
+ Gọi $S'$ là diện tích tam giác khi tăng cạnh $BC$ lên $2$ lần đồng thời tăng cạnh $CA$ lên $3$ lần và giữ nguyên độ lớn của góc $C$ , ta có: \(S' = \dfrac{1}{2}.2BC.3CA.\sin C = 6S\)
Tam giác $ABC$ có $BC = 10$ và \(\widehat A = {30^0}\). Khi đó, bán kính đường tròn ngoại tiếp tam giác $ABC$ là:
Từ \(\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{BC}}{{2\sin A}} = \dfrac{{10}}{{2\sin {{30}^0}}} = 10\)
Tam giác vuông cân tại $A$ có $AB = 2a$. Đường trung tuyến $BM$ có độ dài là:
+ Ta có $AB = AC = 2a$ .
+ Ta có \(BC = \sqrt {A{B^2} + A{C^2}} = \sqrt {4{a^2} + 4{a^2}} = 2\sqrt 2 a\)
+ \(MB_{}^2 = \dfrac{{B{C^2} + A{B^2}}}{2} - \dfrac{{A{C^2}}}{4} = \dfrac{{8{a^2} + 4{a^2}}}{2} - \dfrac{{4{a^2}}}{4} = 5{a^2} \Rightarrow MB = a\sqrt 5 \)

