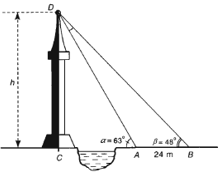
. Giả sử \(CD = h\) là chiều cao của tháp trong đó \(C\) là chân tháp. Chọn hai điểm \(A,{\rm{ }}B\) trên mặt đất sao cho ba điểm \(A,{\rm{ }}B\) và \(C\) thẳng hàng. Ta đo được \(AB = 24{\rm{ m}}\), \(\widehat {CAD} = {63^0},{\rm{ }}\widehat {CBD} = {48^0}\).

                Chiều cao \(h\) của tháp gần với giá trị nào sau đây?  

\( R = \dfrac{a}{{\sin A}}\)

\( R = \dfrac{{\sqrt 2 }}{2}b\)

\( R = \dfrac{{\sqrt 2 }}{2}c\)

\( R = \dfrac{{\sqrt 2 }}{2}a\)

\( S = \dfrac{1}{2}ca\)

\( S = \dfrac{{ - \sqrt 2 }}{4}ac\)

 \( S = \dfrac{{\sqrt 2 }}{4}bc\)

\( S = \dfrac{{\sqrt 2 }}{4}ca\)

\( {a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)

\( \dfrac{b}{{\sin A}} = \dfrac{a}{{\sin B}}\)

\( \sin B = \dfrac{{ - \sqrt 2 }}{2}\)

\( {b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)

\( \sin A = \sin \,(B + C)\)

\( \cos A = \cos \,(B + C)\)

\( \;\cos A > 0\)

\( \sin A\,\, \le 0\)

\( S = \dfrac{{abc}}{{4r}}\)

\( r = \dfrac{{2S}}{{a + b + c}}\)

\( {a^2} = {b^2} + {c^2} + 2bc\;\cos A\)

\( S = r\,(a + b + c)\)

13,114

12,104

11,154

10,151