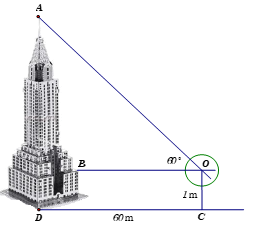
Xác định chiều cao của một tháp mà không cần lên đỉnh của tháp. Đặt kế giác thẳng đứng cách chân tháp một khoảng \(CD = 60{\rm{m}}\), giả sử chiều cao của giác kế là \(OC = 1{\rm{m}}\). Quay thanh giác kế sao cho khi ngắm theo thanh ta nhình thấy đỉnh \(A\) của tháp. Đọc trên giác kế số đo của góc \(\widehat {AOB} = {60^0}\). Chiều cao của ngọn tháp gần với giá trị nào sau đây:   

\( R = \dfrac{a}{{\sin A}}\)

\( R = \dfrac{{\sqrt 2 }}{2}b\)

\( R = \dfrac{{\sqrt 2 }}{2}c\)

\( R = \dfrac{{\sqrt 2 }}{2}a\)

\( S = \dfrac{1}{2}ca\)

\( S = \dfrac{{ - \sqrt 2 }}{4}ac\)

 \( S = \dfrac{{\sqrt 2 }}{4}bc\)

\( S = \dfrac{{\sqrt 2 }}{4}ca\)

\( {a^2} = {b^2} + {c^2} + \sqrt 2 ab.\)

\( \dfrac{b}{{\sin A}} = \dfrac{a}{{\sin B}}\)

\( \sin B = \dfrac{{ - \sqrt 2 }}{2}\)

\( {b^2} = {c^2} + {a^2} - 2ca\cos {135^o}.\)

\( \sin A = \sin \,(B + C)\)

\( \cos A = \cos \,(B + C)\)

\( \;\cos A > 0\)

\( \sin A\,\, \le 0\)

\( S = \dfrac{{abc}}{{4r}}\)

\( r = \dfrac{{2S}}{{a + b + c}}\)

\( {a^2} = {b^2} + {c^2} + 2bc\;\cos A\)

\( S = r\,(a + b + c)\)

13,114

12,104

11,154

10,151