Cho góc \(\widehat {xOy} = 30^\circ \). Gọi \(A\) và \(B\) là hai điểm di động lần lượt trên \(Ox\) và \(Oy\) sao cho \(AB = 1\). Khi \(OB\) có độ dài lớn nhất thì độ dài của đoạn \(OA\) bằng:
Trả lời bởi giáo viên
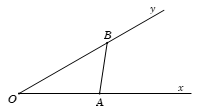
Theo định lí hàm sin, ta có
\(\dfrac{{OB}}{{\sin \widehat {OAB}}} = \dfrac{{AB}}{{\sin \widehat {AOB}}}\)\( \Leftrightarrow OB = \dfrac{{AB}}{{\sin \widehat {AOB}}}.\sin \widehat {OAB}\) \( = \dfrac{1}{{\sin 30^\circ }}.\sin \widehat {OAB} = 2\sin \widehat {OAB}\)
Do đó, độ dài \(OB\) lớn nhất khi và chỉ khi \(\sin \widehat {OAB} = 1 \Leftrightarrow \widehat {OAB} = 90^\circ \).
Khi đó \(OB = 2\).
Tam giác \(OAB\) vuông tại \(A\)\( \Rightarrow OA = \sqrt {O{B^2} - A{B^2}} = \sqrt {{2^2} - {1^2}} = \sqrt 3 \)
Hướng dẫn giải:
Sử dụng định lý hàm số sin cho tam giác \(OAB\) và đánh giá GTLN của \(OB\), từ đó suy ra độ dài của \(OA\).

