Câu hỏi:
3 năm trước
Tam giác \(ABC\) có \(AB = 4,\;BC = 6,\;AC = 2\sqrt 7 \). Điểm \(M\) thuộc đoạn \(BC\) sao cho \(MC = 2MB\). Tính độ dài cạnh \(AM\).
Trả lời bởi giáo viên
Đáp án đúng: c
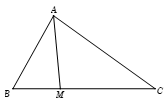
Theo định lí hàm cosin, ta có : \(\cos B = \dfrac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}}\) \( = \dfrac{{{4^2} + {6^2} - {{\left( {2\sqrt 7 } \right)}^2}}}{{2.4.6}} = \dfrac{1}{2}\).
Do \(MC = 2MB \Rightarrow BM = \dfrac{1}{3}BC = 2\).
Theo định lí hàm cosin, ta có
\(A{M^2} = A{B^2} + B{M^2} - 2.AB.BM.\cos \widehat B\)\( = {4^2} + {2^2} - 2.4.2.\dfrac{1}{2} = 12\)
\( \Rightarrow AM = 2\sqrt 3 \)
Hướng dẫn giải:
- Tính \(\cos B = \dfrac{{A{B^2} + B{C^2} - A{C^2}}}{{2.AB.BC}}\)
- Sử dụng định lý cô sin trong tam giác \(ABM\) để tính \(AM\).

