Câu hỏi:
3 năm trước
Tam giác \(ABC\) có \(AB = 9\)cm, \(AC = 12\)cm và \(BC = 15\)cm. Tính độ dài đường trung tuyến \(AM\) của tam giác đã cho
Trả lời bởi giáo viên
Đáp án đúng: a
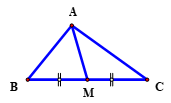
Áp dụng hệ thức đường trung tuyến \(m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\) ta được:
\(m_a^2 = \dfrac{{A{C^2} + A{B^2}}}{2} - \dfrac{{B{C^2}}}{4} = \dfrac{{{{12}^2} + {9^2}}}{2} - \dfrac{{{{15}^2}}}{4} = \dfrac{{225}}{4}.\)
\( \Rightarrow {m_a} = \dfrac{{15}}{2}.\)
Hướng dẫn giải:
Sử dụng công thức trung tuyến \(m_a^2 = \dfrac{{{b^2} + {c^2}}}{2} - \dfrac{{{a^2}}}{4}\).

