Hàm số bậc nhất

Tọa độ giao điểm $A$ của hai đường thẳng $\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)$ là nghiệm của hệ phương trình $\left\{ \begin{array}{l}y = 2x - 3\\y = x - 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = 2\\y = 1\end{array} \right. \Rightarrow A\left( {2;\,\,1} \right)$.

Để ba đường thẳng $\left( {{d_1}} \right),\,\,\left( {{d_2}} \right),\,\,\left( {{d_3}} \right)$ đồng quy thì tọa độ điểm $A$ phải thỏa mãn phương trình đường thẳng $\left( {{d_3}} \right)$ hay \(A \in \left( {{d_3}} \right)\).

Tức là  $1 = \left( {m - 1} \right).2 + 2 \Leftrightarrow m = \dfrac{1}{2}$.

Vì đường thẳng (d) tạo với trục Ox  một góc ${120^0}$ nên hệ số góc k của đường thẳng (d) là $k = \tan {120^0} =  - \sqrt 3 $.

Suy ra phương trình đường thẳng (d) có dạng $y =  - \sqrt 3 x + b$.

Lại có $A \in \left( d \right)$ nên có đẳng thức $ - 5 =  - \sqrt 3 \left( { - 1} \right) + b \Leftrightarrow b =  - \sqrt 3  - 5$.

Với $b =  - \sqrt 3  - 5$ thì $d:\,\,y =  - \sqrt 3 x - \sqrt 3  - 5$.

Để hàm số đã cho đồng biến trên $R$ thì ${m^2} - 1 > 0 \Leftrightarrow \left[ \begin{array}{l}m <  - 1\\m > 1\end{array} \right.$.

Kết hợp với điều kiện $m \in \left[ {0;\,\,3} \right] \Rightarrow m \in \left( {1;3} \right]$ thì có hai giá trị nguyên là $m = 2$ và $m = 3.$

Để hai đường thẳng cắt nhau ta cần có $m \ne  - 2$.

Gọi $A$ là giao điểm của $(d)$ và $(d’).$ Khi đó, tọa độ của $A$ là nghiệm của hệ phương trình:

$\left\{ \begin{array}{l}y =  - 2x + 3\\y = mx + 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{2}{{2 + m}}\\y = \dfrac{{2 + 3m}}{{2 + m}}\end{array} \right. $ $\Rightarrow A\left( {\dfrac{2}{{2 + m}};\,\,\dfrac{{2 + 3m}}{{2 + m}}\,\,} \right)$

Đường phân giác góc thứ hai là $y = – x .$

Để $A$ thuộc đường phân giác góc thứ hai thì đẳng thức ${y_A} =  - {x_A}$ phải thỏa mãn.

Điều này tương đương $\dfrac{{2 + 3m}}{{2 + m}} =  - \dfrac{2}{{2 + m}}(m\ne -2)$ $ \Rightarrow 2 + 3m =  - 2 \Leftrightarrow m =  - \dfrac{4}{3}(TM)$

Điểm $A\left( {{x_0};\,\,{y_0}} \right)$ là điểm cố định thuộc (d) khi và chỉ khi ${y_0} = 2m{x_0} - m + 1\,\,\,\,\left( {\forall m} \right)$

Tương đương $\left( {2{x_0} - 1} \right)m - {y_0} + 1 = 0\,\,\,\,\,\left( {\forall m} \right)\,\,\,\,\,\left( * \right)$

Đẳng thức $\left( * \right)$ xảy ra khi và chỉ khi $\left\{ \begin{array}{l}2{x_0} - 1 = 0\\ - {y_0} + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_0} = \dfrac{1}{2}\\{y_0} = 1\end{array} \right.$.

Do đó, $A\left( {\dfrac{1}{2};\,\,1} \right)$ là điểm cố định mà họ đường thẳng (d) luôn đi qua.

Thấy rằng $m \ne 1$ vì nếu $m = 1$ thì đường thẳng $(d)$ suy biến thành $y = – 4 $ có đồ thị song song với trục hoành và không cắt trục hoành.

Phương trình hoành độ giao điểm của $(d)$ và trục hoành là: $2\left( {m - 1} \right)x - {m^2} - 3 = 0 \Rightarrow x = \dfrac{{{m^2} + 3}}{{2\left( {m - 1} \right)}}$

Do $x<2$ nên $\dfrac{{{m^2} + 3}}{{2\left( {m - 1} \right)}} < 2$ $ \Leftrightarrow  \dfrac{{{m^2} + 3}}{{2\left( {m - 1} \right)}} - 2<0$ $ \Leftrightarrow \dfrac{{{m^2} - 4m + 7}}{{m - 1}} < 0 $ $\Leftrightarrow m - 1 < 0 $ $\Leftrightarrow m < 1$ 

(Vì \({m^2} - 4m + 7 = {\left( {m - 2} \right)^2} + 3 > 0\,\,\forall m\))

Trước hết nhận xét rằng: $2 > 0$ nên hàm số đã cho đồng biến trên $\left[ {1;\,\,3} \right]$.

Với $1 \le {x_1} < {x_2} \le 3 $ $\Rightarrow y\left( 1 \right) \le y\left( {{x_1}} \right) < y\left( {{x_2}} \right) \le y\left( 3 \right)$ nên giá trị lớn nhất của hàm số đã cho đạt được tại $x = 3.$

Khi đó ${y_{max}} = y\left( 3 \right) = 2.3 + {m^2} - 1 = 5 + {m^2}$

Để ${y_{max}} = 5$ thì $5 + {m^2} = 5 \Leftrightarrow m = 0$

Thấy rằng hai đường thẳng $\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)$ không vuông góc với nhau nên đường thẳng $(d)$ cần xác đinh phải vuông góc với một trong hai đường thẳng $\left( {{d_1}} \right),\,\,\left( {{d_2}} \right)$.

Gọi phương trình đường thẳng $(d)$ có dạng $y = ax + b\,\,\,\left( {a \ne 0} \right)$.

TH1: Đường thẳng $(d)$ vuông góc với $\left( {{d_1}} \right)$ suy ra $a.1 =  - 1 \Leftrightarrow a =  - 1$ hay $(d)$ có dạng $y = – x + b .$

Thay tọa độ điểm $A\left( {1;\,\,1} \right)$ vào $(d)$ suy ra $b = 2.$ Khi đó, $(d): y = – x + 2.$

TH2: Đường thẳng $(d)$ vuông góc với $\left( {{d_2}} \right)$ suy ra $a =  - \dfrac{1}{4}$ hay $(d) $ có dạng $y =  - \dfrac{1}{4}x + b$

Thay tọa độ điểm $A\left( {1;\,\,1} \right)$ vào $(d)$  suy ra $b = \dfrac{5}{4}.$ Khi đó,  $\left( d \right):\,\,\,y =  - \dfrac{1}{4}x + \dfrac{5}{4}$

Vậy có hai đường thẳng thỏa mãn $\left( d \right):\,\,\,y =  - x + 2;\,\,\left( d \right):\,\,\,y =  - \dfrac{1}{4}x + \dfrac{5}{4}.$

Hoành độ giao điểm hai đường thẳng $\left( {{d_1}} \right)$ và $\left( {{d_2}} \right)$ là nghiệm của phương trình:

$mx + 1 = 2x + 3 \Leftrightarrow \left( {m - 2} \right)x = 2 \Leftrightarrow \left\{ \begin{array}{l}m \ne 2\\x = \dfrac{2}{{m - 2}}\end{array} \right.$

Tọa độ giao điểm là số nguyên khi và chỉ khi $\dfrac{2}{{m - 2}}$ nhận giá trị nguyên.

Từ đây suy ra $\left( {m - 2} \right) \in \left\{ { \pm 1;\,\, \pm 2} \right\}$

Với $m-2 =  - 1 \Rightarrow m = 1$

Với $m-2 = 1 \Rightarrow m = 3$

Với $m-2 = 2 \Rightarrow m = 4$

Với $m-2=  - 2 \Rightarrow m = 0$

Vậy \(m\in \{0;1;3;4\}\).

Vì đường thẳng $\left( d \right)$  song song với đường thẳng $y =  - \dfrac{2}{3}x + 1$ nên hệ số góc $a =  - \dfrac{2}{3}$.

Suy ra $\left( d \right)$  có dạng $y =  - \dfrac{2}{3}x + b$.

Điểm $M\left( {4;\,\, - 3} \right)$ thuộc $\left( d \right)$  nên tọa độ điểm $M$  phải thỏa mãn đẳng thức $ - 3 =  - \dfrac{2}{3}.4 + b \Rightarrow b =  - \dfrac{1}{3}$.

Do đó ${a^2} + {b^3} = \dfrac{{11}}{{27}}$.

Xét mệnh đề i):

\(y = f\left( x \right)\) và \(y = g\left( x \right)\) là những hàm số chẵn thì $f\left( x \right) = f\left( { - x} \right),\,\,g\left( x \right) = g\left( { - x} \right),\,\,\forall x \in R$

Suy ra  $f\left( x \right) + g\left( x \right) = f\left( { - x} \right) + g\left( { - x} \right)\,,\,\,\forall x \in \mathbb{R} \Rightarrow S\left( x \right) = S\left( { - x} \right),\,\,\,\forall x \in R$

$f\left( x \right)g\left( x \right) = f\left( { - x} \right)g\left( { - x} \right),\,\,\forall x \in \mathbb{R} \Rightarrow P\left( x \right) = P\left( { - x} \right),\,\,\,\forall x \in R$

Do đó \(y = S\left( x \right)\) và \(y = P\left( x \right)\) cũng là những hàm số chẵn.

Vậy mệnh đề i) đúng.

Xét mệnh đề ii):

\(y = f\left( x \right)\) và \(y = g\left( x \right)\) là những hàm số lẻ thì $ - f\left( x \right) = f\left( { - x} \right),\,\, - g\left( x \right) = g\left( { - x} \right),\,\,\forall x \in R$

Suy ra $ - \left( {f\left( x \right) + g\left( x \right)} \right) = f\left( { - x} \right) + g\left( { - x} \right)\,,\,\,\forall x \in \mathbb{R} \Rightarrow  - S\left( x \right) = S\left( { - x} \right),\,\,\,\forall x \in R$ do đó \(y = S\left( x \right)\) là hàm số lẻ.

Lại có $f\left( x \right)g\left( x \right) = f\left( { - x} \right)g\left( { - x} \right),\,\,\forall x \in \mathbb{R} \Rightarrow P\left( x \right) = P\left( { - x} \right),\,\,\,\forall x \in R$ nên \(y = P\left( x \right)\) là hàm số chẵn.

Vậy mệnh đề ii) đúng.

Xét mệnh đề iii):

\(y = f\left( x \right)\) là hàm số chẵn, \(y = g\left( x \right)\) là hàm số lẻ thì $f\left( x \right) = f\left( { - x} \right),\,\, - g\left( x \right) = g\left( { - x} \right),\,\,\forall x \in R$

Suy ra $ - f\left( x \right)g\left( x \right) = f\left( { - x} \right)g\left( { - x} \right),\,\,\forall x \in \mathbb{R} \Rightarrow  - P\left( x \right) = P\left( { - x} \right),\,\,\,\forall x \in R$ nên \(y = P\left( x \right)\) là hàm số lẻ.

Vậy mệnh đề iii) đúng.

Vậy số mệnh đề đúng là $3$.

Thay $x = 1$ vào phương trình đường thẳng $\left( {{d_1}} \right)$ ta có ${y_A} = m - 1 \Rightarrow A\left( {1;\,\,m - 1} \right).$

Thay $x = 2$ vào phương trình đường thẳng $\left( {{d_2}} \right)$ ta có ${y_B} = 3 - 2m \Rightarrow B\left( {2;\,\,3 - 2m} \right).$

Hai điểm $A$ và $B$ nằm về hai phía của trục hoành khi và chỉ khi ${y_A}.{y_B} < 0 \Leftrightarrow \left( {m - 1} \right)\left( {3 - 2m} \right) < 0 \Leftrightarrow \left[ \begin{array}{l}m > \dfrac{3}{2}\\m < 1\end{array} \right.$

Gọi $A\left( {x;\,\,1 + 3x} \right) \in \left( d \right)$.

Tọa độ điểm A thỏa mãn phương trình $6x + {y^2} = 5y$ khi và chỉ khi:

$\begin{array}{l}6x + {\left( {1 + 3x} \right)^2} = 5\left( {1 + 3x} \right)\\ \Leftrightarrow 6x + 1 + 6x + 9{x^2} = 5 + 15x\\ \Leftrightarrow 9{x^2} - 3x - 4 = 0\\ \Leftrightarrow x = \dfrac{{1 \pm \sqrt {17} }}{6}\end{array}$

Thay vào phương trình đường thẳng (d) ta tìm được hai điểm thỏa mãn là

$\left( {\dfrac{{1 + \sqrt {17} }}{6};\,\,\dfrac{{3 + \sqrt {17} }}{2}} \right)$ và $\left( {\dfrac{{1 - \sqrt {17} }}{6};\,\,\dfrac{{3 - \sqrt {17} }}{2}} \right)$.

Để đường thẳng \(\Delta \) vuông góc với đường thẳng \(d\) khi và chỉ khi \(2\left( {3m + 2} \right) =  - 1 \Leftrightarrow m =  - \dfrac{5}{6}\).

Ta có $y = \left| {x + 1} \right| + \left| {x - 1} \right| = \left\{ \begin{array}{l} - 2x\,\,\,\left( {x <  - 1} \right)\\2\,\,\,\,\,\,\left( { - 1 \le x \le 1} \right)\\2x\,\,\,\,\left( {x \ge 1} \right)\end{array} \right.$ và có đồ thị chính là phần đường thẳng màu xanh như sau:

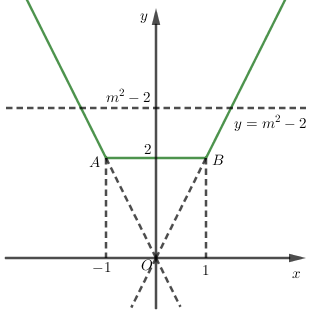
Đường thẳng $d:\,\,y = {m^2} - 2$ song song với trục hoành.

Số nghiệm của phương trình bằng số giao điểm của đồ thị hàm số $y = \left\{ \begin{array}{l} - 2x\,\,\,\left( {x <  - 1} \right)\\2\,\,\,\,\,\,\left( { - 1 \le x \le 1} \right)\\2x\,\,\,\,\left( {x \ge 1} \right)\end{array} \right.$ và đường thẳng $d:\,\,y = {m^2} - 2$.

Nhìn vào đồ thị ta thấy đường thẳng $y=m^2-2$ chỉ cắt đồ thị hàm số (đường màu xanh) tại $2$ điểm phân biệt khi $m^2-2>2$

Hay phương trình đã cho có hai nghiệm phân biệt khi ${m^2} - 2 > 2 \Rightarrow {m^2} > 4 \Leftrightarrow \left[ \begin{array}{l}m <  - 2\\m > 2\end{array} \right.$.

Bước 1:

Gọi $A$ và $B$  lần lượt là giao điểm của đường thẳng $\left( d \right)$ với trục $Ox,Oy$ .

Khi đó, $A\left( {\dfrac{{m - 1}}{m};\,\,0} \right),\,\,\,\,B\left( {0;\,\, - m + 1} \right)$.

Gọi H là hình chiều của $O$ lên đường thẳng $\left( d \right)$ thì $OH$ chính là khoảng cách từ điểm $O$ tới đường thẳng $\left( d \right)$ .

Xét tam giác vuông $OAB$ có $\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} \Leftrightarrow OH = \dfrac{{OA.OB}}{{\sqrt {O{A^2} + O{B^2}} }}$.

Suy ra $O{H_{\min }} \Leftrightarrow {\left( {\dfrac{{OA.OB}}{{\sqrt {O{A^2} + O{B^2}} }}} \right)_{\min }}$.

Ta có $\dfrac{{OA.OB}}{{\sqrt {O{A^2} + O{B^2}} }} = \dfrac{{\left| {\dfrac{{m - 1}}{m}} \right|\left| { - m + 1} \right|}}{{\sqrt {{{\left( {\dfrac{{m - 1}}{m}} \right)}^2} + {{\left( {m - 1} \right)}^2}} }} = \dfrac{{{{\left( {m - 1} \right)}^2}}}{{\sqrt {{{\left( {m - 1} \right)}^2}\left( {1 + {m^2}} \right)} }} = \dfrac{{\left| {m - 1} \right|}}{{\sqrt {1 + {m^2}} }}$

Bước 2:

Theo bất đẳng thức Cauchy-Schwarz, ta có:

$\left| {m - 1} \right| =\left| {1.m +(- 1).1} \right|$$\le \sqrt{1^2+(-1)^2}.\sqrt{1^2+m^2}$

$=>\dfrac{{\left| {m - 1} \right|}}{{\sqrt {1 + {m^2}} }} $$\le \dfrac{{\sqrt 2 \sqrt {1 + {m^2}} }}{{\sqrt {1 + {m^2}} }} = \sqrt 2 $.

Dấu "=" xảy ra khi $\dfrac{1}{-1}=\dfrac{m}{1}\Leftrightarrow m=-1$

Vậy $O{H_{\min }} = \sqrt 2 $ và đạt được khi $m =  - 1$.

TH1:

\(\left| {2x + 10} \right| = 2x + 10\) khi \(2x + 10 \ge 0 \Leftrightarrow x \ge  - 5\)

TH2:

\(\left| {2x + 10} \right| =  - \left( {2x + 10} \right) =  - 2x - 10\) khi \(2x + 10 < 0 \Leftrightarrow x <  - 5\).

Vậy \(y = \left\{ \begin{array}{l}2x + 10,\,\,\,khi\,x \ge  - 5\\ - 2x - 10,\,\,\,khi\,x <  - 5\end{array} \right.\)

Trong các đáp án chỉ có hàm số \(y = 2x - 4\) là hàm số bậc nhất.

Ta có:

\(\left| {3 + x} \right| \ge 0,\,\,\forall x \Leftrightarrow \left| {3 + x} \right| - 1 \ge  - 1,\,\,\forall x \in \mathbb{R}\)

\(\Rightarrow \) Tập giá trị của hàm số \(y = \left| {3 + x} \right| - 1\) là: \(\left[ { - 1; + \infty } \right)\).

+) Xét đáp án A: \(y =  - 2 + 3x\) có \(a = 3 > 0 \Rightarrow \) hàm số đồng biến trên \(\mathbb{R}.\)