Khoảng cách và góc

\(\begin{array}{l}d\left( {M;\,\,\Delta } \right) = \dfrac{{\left| { - m + 2 - m + 4} \right|}}{{\sqrt {{m^2} + 1} }} = 2\sqrt 5 \\ \Leftrightarrow \dfrac{{\left| { - 2m + 6} \right|}}{{\sqrt {{m^2} + 1} }} = 2\sqrt 5  \Leftrightarrow \dfrac{{\left| {m - 3} \right|}}{{\sqrt {{m^2} + 1} }} = \sqrt 5 \\ \Leftrightarrow {\left( {m - 3} \right)^2} = 5\left( {{m^2} + 1} \right)\\ \Leftrightarrow {m^2} - 6m + 9 = 5{m^2} + 5\\ \Leftrightarrow 4{m^2} + 6m - 4 = 0 \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{1}{2}\\m =  - 2\end{array} \right..\end{array}\)

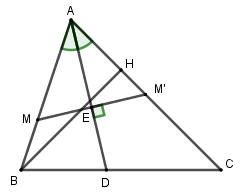
Lấy điểm \(M'\) đối xứng với \(M\) qua \(AD\) thì \(M' \in AC\).

+) Viết phương trình \(MM'\).

\(AD:x - y + 1 = 0\) có \(\overrightarrow {{n_{AD}}}  = \left( {1; - 1} \right) \Rightarrow \overrightarrow {{u_{AD}}}  = \left( {1;1} \right)\).

Ta có: \(MM' \bot AD\) \( \Rightarrow \overrightarrow {{n_{MM'}}}  = \overrightarrow {{u_{AD}}}  = \left( {1;1} \right)\)

Đường thẳng \(MM'\) đi qua \(M\left( {0;2} \right)\) và nhận \(\overrightarrow {{n_{MM'}}}  = \left( {1;1} \right)\) làm VTPT nên:

\(MM':1\left( {x - 0} \right) + 1\left( {y - 2} \right) = 0\) hay \(x + y - 2 = 0\).

Gọi \(E = MM' \cap AD\), tọa độ \(E\) thỏa mán hệ phương trình \(\left\{ \begin{array}{l}x - y + 1 = 0\\x + y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{1}{2}\\y = \dfrac{3}{2}\end{array} \right.\) \( \Rightarrow {\rm{E}}\left( {\dfrac{1}{2};\dfrac{3}{2}} \right)\).

Mà \(E\) là trung điểm của \(MM'\) nên \(\left\{ \begin{array}{l}{x_{M'}} = 2{x_E} - {x_M} = 1\\{y_{M'}} = 2{y_E} - {y_M} =  - 1\end{array} \right.\) \( \Rightarrow M'\left( {1;1} \right)\).

Ta có: \(BH:3x + 4y + 10 = 0\) \( \Rightarrow \overrightarrow {{n_{BH}}}  = \left( {3;4} \right) \Rightarrow \overrightarrow {{u_{BH}}}  = \left( {4; - 3} \right)\), \(AC \bot BH \Rightarrow \overrightarrow {{n_{AC}}}  = \overrightarrow {{u_{BH}}}  = \left( {4; - 3} \right)\).

Đường thẳng \(AC\) đi qua \(M'\left( {1;1} \right)\) và nhận \(\overrightarrow {{n_{AC}}}  = \left( {4; - 3} \right)\) làm VTPT nên:

\(AC:4\left( {x - 1} \right) - 3\left( {y - 1} \right) = 0\) hay \(4x - 3y - 1 = 0\).

\(C \in AC\) nên gọi tọa độ của \(C\left( {t;\dfrac{{4t - 1}}{3}} \right)\) với \(t \in \mathbb{Z}\).

\(MC = \sqrt 2 \) \( \Leftrightarrow \sqrt {{{\left( {t - 0} \right)}^2} + {{\left( {\dfrac{{4t - 1}}{3} - 2} \right)}^2}}  = \sqrt 2 \) \( \Leftrightarrow {t^2} + {\left( {\dfrac{{4t - 7}}{3}} \right)^2} = 2\) \( \Leftrightarrow 9{t^2} + 16{t^2} - 56t + 49 - 18 = 0\) \( \Leftrightarrow 25{t^2} - 56t + 31 = 0\) \( \Leftrightarrow \left[ \begin{array}{l}t = \dfrac{{31}}{{25}}\left( L \right)\\t = 1\left( {TM} \right)\end{array} \right.\)

Vậy hoành độ nguyên của \(C\) là \(1\).

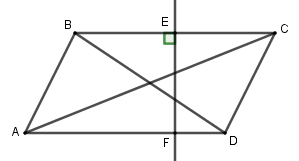
Từ hình vẽ: \(BD:7x + 4y - 5 = 0\), \(EF:2x + 8y - 5 = 0\).

Ta có : \(EF:2x + 8y - 5 = 0\) \( \Rightarrow \overrightarrow {{n_{EF}}}  = \left( {2;8} \right) \Rightarrow \overrightarrow {{u_{EF}}}  = \left( {8; - 2} \right)\).

Đường thẳng \(AD\) đi qua \(A\left( {4;0} \right)\) và vuông góc \(EF\) nên có VTPT \(\overrightarrow {{n_{AD}}}  = \dfrac{1}{2}\overrightarrow {{u_{EF}}}  = \left( {4; - 1} \right)\), khi đó

\(AD:4\left( {x - 4} \right) - \left( {y - 0} \right) = 0\) \( \Leftrightarrow 4x - y - 16 = 0\).

\(D = AD \cap BD\) nên tọa độ của \(D\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}7x + 4y - 5 = 0\\4x - y - 16 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y =  - 4\end{array} \right.\) hay \(D\left( {3; - 4} \right)\).

Dễ thấy \(BE = \dfrac{1}{2}AD\) \( = \dfrac{1}{2}\sqrt {{{\left( {3 - 4} \right)}^2} + {{\left( { - 4 - 0} \right)}^2}}  = \dfrac{{\sqrt {17} }}{2}\) hay \(d\left( {B,EF} \right) = \dfrac{{\sqrt {17} }}{2}\)

Gọi \(B\left( {t;\dfrac{{5 - 7t}}{4}} \right) \in BD\).

Khi đó \(d\left( {B,EF} \right) = \dfrac{{\sqrt {17} }}{2}\)\( \Leftrightarrow \dfrac{{\left| {2t + \dfrac{{8\left( {5 - 7t} \right)}}{4} - 5} \right|}}{{\sqrt {{2^2} + {8^2}} }} = \dfrac{{\sqrt {17} }}{2}\) \( \Leftrightarrow \dfrac{{\left| { - 12t + 5} \right|}}{{2\sqrt {17} }} = \dfrac{{\sqrt {17} }}{2} \Leftrightarrow \left| { - 12t + 5} \right| = 17\) \( \Leftrightarrow \left[ \begin{array}{l} - 12t + 5 = 17\\ - 12t + 5 =  - 17\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t =  - 1\\t = \dfrac{{11}}{6}\end{array} \right.\) \( \Rightarrow \left[ \begin{array}{l}B\left( { - 1;3} \right)\\B\left( {\dfrac{{11}}{6}; - \dfrac{{47}}{{24}}} \right)\end{array} \right.\).

Xét điểm \(B\left( { - 1;3} \right)\) ta thấy : \(\left( {2.4 + 8.0 - 5} \right)\left( {2.\left( { - 1} \right) + 8.3 - 5} \right) > 0\) nên \(A,B\) cùng phía so với \(EF\) (thỏa mãn).

Xét điểm \(B\left( {\dfrac{{11}}{6}; - \dfrac{{47}}{{24}}} \right)\) ta thấy : \(\left( {2.4 + 8.0 - 5} \right)\left( {2.\dfrac{{11}}{6} + 8.\left( { - \dfrac{{47}}{{24}}} \right) - 5} \right) < 0\) nên \(A,B\) khác phía so với \(EF\) (loại).

Do đó \(B\left( { - 1;3} \right)\).

Đường thẳng \(BC\) song song \(AD\) nên có phương trình dạng \(4x - y + c = 0\) với \(c \ne  - 16\).

\(B\left( { - 1;3} \right) \in BC\) nên \(4.\left( { - 1} \right) - 3 + c = 0 \Leftrightarrow c = 7\) hay \(BC:4x - y + 7 = 0\).

\(E = BC \cap EF\) nên tọa độ \(E\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}2x + 8y - 5 = 0\\4x - y + 7 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - \dfrac{3}{2}\\y = 1\end{array} \right.\) \( \Rightarrow E\left( { - \dfrac{3}{2};1} \right)\).

\(E\) là trung điểm \(BC\) nên \(\left\{ \begin{array}{l}{x_C} = 2{x_E} - {x_B} =  - 2\\{y_C} = 2{y_E} - {y_B} =  - 1\end{array} \right.\) \( \Rightarrow C\left( { - 2; - 1} \right)\).

Vậy \(B\left( { - 1;3} \right),C\left( { - 2; - 1} \right),D\left( {3; - 4} \right)\).

Ta có

+) \(\left( {2.1 - 3.3 + 6} \right)\left( { - 2.2 - 3.4 + 6} \right) = 10 > 0\) nên hai điểm \(A\), \(B\) nằm cùng về một phía của đường thẳng \(d\)\( \Rightarrow \) cạnh \(AB\) không cắt đường thẳng \(d\).

+) \(\left( { - 2.2 - 3.4 + 6} \right)\left( { - 1.2 - 3.5 + 6} \right) = 110 > 0\) nên hai điểm \(B\), \(C\) nằm cùng về một phía của đường thẳng \(d\)\( \Rightarrow \) cạnh \(BC\) không cắt đường thẳng \(d\).

+) \(\left( {2.1 - 3.3 + 6} \right)\left( { - 1.2 - 3.5 + 6} \right) = 11 > 0\) nên hai điểm \(A\), \(C\) nằm cùng về một phía của đường thẳng \(d\)\( \Rightarrow \) cạnh \(AC\) không cắt đường thẳng \(d\).

Vậy đường thẳng \(d\) không cắt cạnh nào của tam giác.

 $\left\{ \begin{align} & {{d}_{1}}:x+2y-7=0\to {{{\vec{n}}}_{1}}=\left( 1;2 \right) \\  & {{d}_{2}}:2x-4y+9=0\to {{{\vec{n}}}_{2}}=\left( 1;-2 \right) \\ \end{align} \right.$ $\xrightarrow{\varphi =\left( {{d}_{1}};{{d}_{2}} \right)}\cos \varphi =\dfrac{\left| 1-4 \right|}{\sqrt{1+4}.\sqrt{1+4}}=\dfrac{3}{5}.$

\(\left\{ \begin{array}{l}{d_1}:6x - 5y + 15 = 0 \to {{\vec n}_1} = \left( {6; - 5} \right)\\{d_2}:\left\{ \begin{array}{l}x = 10 - 6t\\y = 1 + 5t\end{array} \right. \to {{\vec n}_2} = \left( {5;6} \right)\end{array} \right. \to {\vec n_1} \cdot {\vec n_2} = 0 \Rightarrow \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right) = \varphi  = {90^ \circ }.\)

Ta có

   \(\left\{ \begin{array}{l}{d_1}:3x + 4y + 12 = 0 \to {{\vec n}_1} = \left( {3;4} \right)\\{d_2}:\left\{ \begin{array}{l}x = 2 + at\\y = 1 - 2t\end{array} \right. \to {{\vec n}_2} = \left( {2;a} \right)\end{array} \right.\)

\(\varphi  = \left( {{d_1};{d_2}} \right) = {45^0} \Rightarrow \dfrac{1}{{\sqrt 2 }} = \cos {45^0} = \cos \varphi  = \dfrac{{\left| {6 + 4a} \right|}}{{\sqrt {25} .\sqrt {{a^2} + 4} }}\)

\( \Leftrightarrow 25\left( {{a^2} + 4} \right) = 8\left( {4{a^2} + 12a + 9} \right) \Leftrightarrow 7{a^2} + 96a - 28 = 0 \Leftrightarrow \left[ \begin{array}{l}a =  - 14\\a = \dfrac{2}{7}\end{array} \right..\)

Công thức tính khoảng cách từ một điểm đến đường thẳng:

\(d\left( {M,\Delta } \right) = \,\dfrac{{\left| {\left. {a{x_0} + b{y_0} + c} \right|} \right.}}{{\sqrt {{a^2} + {b^2}} }}.\)

Tọa độ giao điểm A của hai đường thẳng x-3y+4=0 và 2x+3y-1=0 thỏa mãn hệ phương trình:

\(\left\{ \begin{array}{l}x - 3y + 4 = 0\\2x + 3y - 1 = 0\end{array} \right. \)

$ \Leftrightarrow \left\{ \begin{array}{l}
x - 3y = - 4\\
2x + 3y = 1
\end{array} \right.$

\(\Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 1\end{array} \right. \)

\(\to A\left( { - 1;1} \right) \)

\(\to d\left( {A;\Delta } \right) = \dfrac{{\left| { - 3 + 1 + 4} \right|}}{{\sqrt {9 + 1} }} = \dfrac{2}{{\sqrt {10} }}.\)

$\left\{ \begin{array}{l}A\left( {1;2} \right)\\B\left( {0;3} \right),\,\,C\left( {4;0} \right) \end{array} \right.\\\to BC:3(x-0) + 4(y - 3) =3x+4y-12= 0\\ \to {h_A} = d\left( {A;BC} \right) = \dfrac{{\left| {3 + 8 - 12} \right|}}{{\sqrt {9 + 16} }} = \dfrac{1}{5}.$

Cách 1:

+) Viết phương trình \(BC\):

Ta có: \(\overrightarrow {BC}  = \left( {2; - 4} \right)\) nên \(\overrightarrow {{u_{BC}}}  = \dfrac{1}{2}\overrightarrow {BC}  = \left( {1; - 2} \right)\) là VTCP của \(BC\), do đó \(\overrightarrow {{n_{BC}}}  = \left( {2;1} \right)\).

Đường thẳng \(BC\) đi qua \(B\left( {1;5} \right)\) và nhận \(\overrightarrow {{n_{BC}}}  = \left( {2;1} \right)\) làm VTPT nên: \(BC:2\left( {x - 1} \right) + 1\left( {y - 5} \right) = 0\) hay \(BC:2x + y - 7 = 0\).

Suy ra $\left\{ \begin{array}{l}A\left( {3; - 4} \right)\\B\left( {1;5} \right),\,C\left( {3;1} \right)\end{array} \right. \to \left\{ \begin{array}{l}A\left( {3; - 4} \right)\\BC = 2\sqrt 5 \\BC:2x + y - 7 = 0\end{array} \right. \to \left\{ \begin{array}{l}BC = 2\sqrt 5 \\{h_A} = d\left( {A;BC} \right) = \sqrt 5 \end{array} \right.$

 $ \to {S_{ABC}} = \dfrac{1}{2}.2\sqrt 5 .\sqrt 5  = 5.$

$d\left( {A;\Delta } \right) = \dfrac{{\left| { - m + 2 - m + 4} \right|}}{{\sqrt {{m^2} + 1} }} = 2\sqrt 5 $ $ \Leftrightarrow \left| {m - 3} \right| = \sqrt 5 .\sqrt {{m^2} + 1} $ $ \Leftrightarrow 4{m^2} + 6m - 4 = 0$ $ \Leftrightarrow \left[ \begin{array}{l}m =  - 2\\m = \dfrac{1}{2}\end{array} \right..$

+) TH1: \(\left( d \right)\) không có hệ số góc.

Khi đó phương trình \(\left( d \right)\) có dạng: \(x - c = 0\).

\(\left( d \right)\) đi qua \(M\left( {1;2} \right)\) nên \(x - 1 = 0\) nên có VTPT \(\overrightarrow n  = \left( {1;0} \right)\).

\( \Rightarrow \cos \left( {d,\Delta } \right) = \dfrac{{\left| {\overrightarrow {{n_\Delta }} .\overrightarrow {{n_d}} } \right|}}{{\left| {\overrightarrow {{n_\Delta }} } \right|.\left| {\overrightarrow {{n_d}} } \right|}}\) \( = \dfrac{{\left| {3.1 - 2.0} \right|}}{{\sqrt {{3^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{1^2} + {0^2}} }} = \dfrac{1}{{\sqrt {13} }}\) \( \ne \dfrac{{\sqrt 2 }}{2} = \cos {45^0}\).

Do đó đường thẳng này không thỏa mãn bài toán.

+) TH2: \(\left( d \right)\) có hệ số góc.

PTĐT $\left( d \right)$ được viết dưới dạng: \(y - 2 = k\left( {x - 1} \right) \Leftrightarrow kx - y + 2-k = 0\)

Vì $\left( d \right)$ hợp với $\left( \Delta  \right)$ một góc ${45^0}$ nên: ${\rm{cos 4}}{{\rm{5}}^0} = \dfrac{{|3k + ( - 1).( - 2)|}}{{\sqrt {{k^2} + 1} .\sqrt {{3^2} + {{( - 2)}^2}} }}$ $ \Leftrightarrow \dfrac{{\sqrt 2 }}{2} = \dfrac{{|3k + 2|}}{{\sqrt {13} .\sqrt {{k^2} + 1} }}$ $ \Leftrightarrow \dfrac{2}{4} = \dfrac{{9{k^2} + 12k + 4}}{{13.({k^2} + 1)}}$

\( \Leftrightarrow 5{k^2} + 24k - 5 = 0 \Leftrightarrow \left[ \begin{array}{l}k = \dfrac{1}{5}\\k =  - 5\end{array} \right.\)

Vậy phương trình $\left( d \right)$ là: \(\dfrac{1}{5}x - y + 2 - \dfrac{1}{5} = 0 \Leftrightarrow x - 5y + 9 = 0\) hay \( - 5x - y + 2 - ( - 5) = 0 \Leftrightarrow 5x + y - 7 = 0\)

+) TH1: \(\left( \Delta  \right)\) không có hệ số góc, khi đó phương trình \(\left( \Delta  \right)\) có dạng \(x = c\) hay \(x - c = 0\).

\(\left( \Delta  \right)\) đi qua điểm \(M\left( {2;7} \right)\) nên \(2 - c = 0 \Leftrightarrow c = 2\) \( \Rightarrow \left( \Delta  \right):x - 2 = 0\).

Khi đó \(d\left( {N,\left( \Delta  \right)} \right) = \dfrac{{\left| {1 - 2} \right|}}{{\sqrt {{1^2} + {0^2}} }} = 1\) (thỏa mãn).

Do đó ta có đường thẳng \(\left( {{\Delta _1}} \right):x - 2 = 0\).

+) TH2: \(\left( \Delta  \right)\) có hệ số góc.

PTĐT $\left( \Delta  \right)$  đi qua điểm $M\left( {2;7} \right)$  và có hệ số góc $k$  có dạng là:

$y - 7 = k\left( {x - 2} \right)$\( \Leftrightarrow \)\(kx - y + 7 - 2k = 0\)

Vì $\left( \Delta  \right)$ cách $N\left( {1;2} \right)$ một khoảng bằng $1$  nên:

Ta có: $d(N, ∆) =1$

$\begin{array}{l} \Leftrightarrow \dfrac{{|k.1 - 2 + 7 - 2.k|}}{{\sqrt {{k^2} + 1} }} = 1 \Leftrightarrow \dfrac{{| - k + 5|}}{{\sqrt {{k^2} + 1} }} = 1 \Leftrightarrow {( - k + 5)^2} = {(\sqrt {{k^2} + 1} )^2}\\ \Leftrightarrow {k^2} - 10k + 25 = {k^2} + 1 \Leftrightarrow k = \dfrac{{12}}{5}\end{array}$

Do đó ta có phương trình $\left( \Delta _2 \right)$ là: \(\dfrac{{12}}{5}x - y + 7 - 2.\dfrac{{12}}{5} = 0 \) \(\Leftrightarrow 12x - 5y + 11 = 0\)

Vậy có hai đường thẳng cần tìm là \(\left( {{\Delta _1}} \right):x - 2 = 0\) và \(\left( \Delta _2 \right):12x - 5y + 11 = 0\).

Điểm \(M \in d\) nên tọa độ của $M$  phải thỏa mãn phương trình của $d.$

Gọi \(M(2 + 2t;3 + t) \in d\).

Ta có:$\overrightarrow {AM}  = (2 + 2t;2 + t)$.

Theo giả thiết: \(\overrightarrow {\left| {AM} \right|}  = 5 \Leftrightarrow \sqrt {{{(2 + 2t)}^2} + {{(2 + t)}^2}}  = 5\)\( \Leftrightarrow {(2 + 2t)^2} + {(2 + t)^2} = 25\)

\( \Leftrightarrow 5{t^2} + 12t - 17 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = \dfrac{{ - 17}}{5}\end{array} \right.\).

Vậy có $2$  điểm $M$  thỏa ycbt \({M_1}(4;4)\) và \({M_2}(\dfrac{{ - 24}}{5};\dfrac{{ - 2}}{5})\).

Vì: \(\dfrac{1}{3} \ne \dfrac{3}{1}\) nên $d$  cắt $d'$

 Phương trình hai đường phân giác của các góc tạo bởi $d$ và $d'$ là:

\(\dfrac{{x + 3y - 6}}{{\sqrt {10} }} =  \pm \dfrac{{3x + y + 2}}{{\sqrt {10} }}\)\( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 3y - 6 = 3x + y + 2}\\{x + 3y - 6 =  - \left( {3x + y + 2} \right)}\end{array}} \right.\) \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x - y + 4 = 0}\\{x + y - 1 = 0}\end{array}} \right.\)

+ Cạnh $AB$ đi qua hai điểm $A,B$ nên phương trình cạnh \(AB: x - 2y - 2 = 0\)

+ Cạnh $AC$ đi qua hai điểm $A,C$ nên phương trình cạnh \(AC: 2x + y - 4 = 0\)

+ Phương trình hai đường phân giác của góc $A$:

 \(\dfrac{{x - 2y - 2}}{{\sqrt 5 }} =  \pm \dfrac{{2x + y - 4}}{{\sqrt 5 }} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 3y - 2 = 0\quad \left( d \right)}\\{3x - y - 6 = 0\quad \left( {d'} \right)}\end{array}} \right.\)

+ Xét đường phân giác \(\left( d \right):x + 3y - 2 = 0\)

Thế tọa độ điểm $B$  vào vế trái của \(d\): \({t_1} = 4 + 3.1 - 2 = 5 > 0\)

Thế tạo độ điểm $C$  vào vế trái của \(d\): \({t_2} = 1 + 3.2 - 2 = 5 > 0\)

Vì \({t_1}.{t_2} > 0\) nên $B$  và $C$  nằm cùng phía đối với \(d \Rightarrow d\) là đường phân giác ngoài

Vậy đường phân giác trong của góc $A$  là: \(d':3x - y - 6 = 0\)

Ta thế tọa độ \(M\left( {0;{\rm{ }}1} \right)\) và \(P\left( {0;{\rm{ 2}}} \right)\) vào đường thẳng:

\(\left( {0 - 2.1 + 3} \right)\left( {0 - 2.2 + 3} \right) < 0\) nên loại A.

Ta thế tọa độ \(N\left( {1;{\rm{ 1}}} \right)\) và \(P\left( {0;{\rm{ 2}}} \right)\) vào đường thẳng:

\(\left( {1 - 2.1 + 3} \right)\left( {0 - 2.2 + 3} \right) < 0\) nên loại B.

Ta thế tọa độ \(M\left( {0;{\rm{ }}1} \right)\) và \(Q\left( {2;{\rm{ }} - 1} \right)\) vào đường thẳng:

\(\left( {0 - 2.1 + 3} \right)\left( {2 - 2.\left( { - 1} \right) + 3} \right) > 0\) nên chọn C.

Giả sử đường thẳng $AB$  qua $M$ và có VTPT là $\vec n = \left( {a;b} \right)\,\,\,\,\left( {{a^2} + {b^2} \ne 0} \right)$  

 => VTPT của $BC$ là: ${\vec n_1} = \left( { - b;a} \right)$.

 Phương trình AB có dạng: $a\left( {x-2} \right) + b\left( {y-1} \right) = 0$ $ \Leftrightarrow ax + by-2a-b = 0$

BC có dạng: $-b\left( {x-4} \right) + a\left( {y + 2} \right) = 0\;$ $ \Leftrightarrow -bx + ay + 4b + 2a = 0$

Do $ABCD$ là hình vuông nên  $d\left( {P,AB} \right) = d\left( {Q,BC} \right)$  

 $ \Leftrightarrow \dfrac{{\left| { - b} \right|}}{{\sqrt {{a^2} + {b^2}} }} = \dfrac{{\left| {3b + 4a} \right|}}{{\sqrt {{a^2} + {b^2}} }} \Leftrightarrow \left[ \begin{array}{l}b =  - 2a\\b =  - a\end{array} \right.$

TH1: \(b =  - 2a\)

Chọn \(a = 1 \Rightarrow b =  - 2\) ta được \(AB:x - 2y - 2.1 - \left( { - 2} \right) = 0\) hay \(x - 2y = 0\)

\(BC: - \left( { - 2} \right)x + y + 4.\left( { - 2} \right) + 2.1 = 0\) hay \(2x + y - 6 = 0\)

CD đi qua P(2;0) và song song AB nên nhận \(\overrightarrow {{n_{AB}}}  = \left( {1; - 2} \right)\) làm VTPT

Do đó CD: 1(x-2) – 2(y-0) = 0 hay x-2y-2=0

AD đi qua Q(1;2) và song song BC nên nhận \(\overrightarrow {{n_{BC}}}  = \left( {2;1} \right)\) làm VTPT

Do đó AD: 2(x-1) + 1(y-2) = 0 hay 2x+y-4=0

TH2: \(b =  - a\)

Chọn \(a = 1 \Rightarrow b =  - 1\) ta được \(AB:x - y - 2.1 - \left( { - 1} \right) = 0\) hay \(x - y - 1 = 0\)

\(BC: - \left( { - 1} \right)x + y + 4.\left( { - 1} \right) + 2.1 = 0\) hay \(x + y - 2 = 0\)

CD đi qua P(2;0) và song song AB nên nhận \(\overrightarrow {{n_{AB}}}  = \left( {1; - 1} \right)\) làm VTPT

Do đó CD: 1(x-2) – 1(y-0) = 0 hay x-y-2=0

AD đi qua Q(1;2) và song song BC nên nhận \(\overrightarrow {{n_{BC}}}  = \left( {1;1} \right)\) làm VTPT

Do đó AD: 1(x-1) + 1(y-2) = 0 hay x+y-3=0.

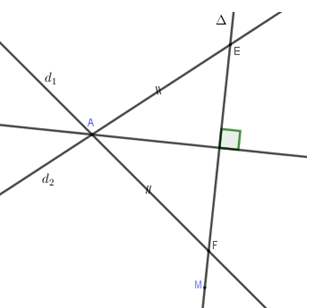
Phương trình đường phân giác góc tạo bởi ${d_1},{d_2}$ là:

$\dfrac{{\left| {x - 7y + 17} \right|}}{{\sqrt {{1^2} + {{( - 7)}^2}} }} = \dfrac{{\left| {x + y - 5} \right|}}{{\sqrt {{1^2} + {1^2}} }}$$ \Leftrightarrow \left[ \begin{array}{l}2x + 6y - 21 = 0{\rm{    (}}{\Delta _1}{\rm{)}}\\3x - y - 4 = 0{\rm{     (}}{\Delta _2}{\rm{)}}\end{array} \right.$

Đường thẳng cần tìm đi qua $M\left( {0;1} \right)$ và vuông góc  với ${\Delta _1},{\Delta _2}$

+ Gọi \({d_3}\) là đường thẳng vuông góc với \({\Delta _1}\) thì \({d_3}\) có dạng: \(3x - y + c = 0\)

\({d_3}\) đi qua điểm \(M\left( {0;1} \right)\) nên \(3.0 - 1 + c = 0 \Leftrightarrow c = 1\) hay \(3x - y + 1 = 0\)

+ Gọi \({d_4}\) là đường thẳng vuông góc với \({\Delta _2}\) thì \({d_4}\) có dạng: \(x + 3y + c = 0\)

\({d_4}\) đi qua điểm \(M\left( {0;1} \right)\) nên \(0 + 3.1 + c = 0 \Leftrightarrow c =  - 3\) hay \(x + 3y - 3 = 0\)

KL: $x + 3y - 3 = 0$ và $3x - y + 1 = 0$