Trong mặt phẳng với hệ tọa độ Oxy, cho ΔABC cân có đáy là BC. Đỉnh A có tọa độ là các số dương, hai điểm B và C nằm trên trục Ox, phương trình cạnh AB: y=3√7(x−1). Biết chu vi của ΔABC bằng 18, tìm tọa độ các đỉnh A,B,C.
B=AB∩Ox⇒B(1;0), A∈AB⇒A(a;3√7(a−1))⇒a>1 (do xA>0,yA>0).
Gọi AH là đường cao ΔABC, do ΔABC cân tại A nên AH cũng là đường trung tuyến, khi đó H là trung điểm của BC
⇒H(a;0)⇒C(2a−1;0)⇒BC=2(a−1),AB=AC=8(a−1)
Chu vi tam giác ABC bằng 18 ⇔a=2⇒C(3;0),A(2;3√7)
Trong mặt phẳng với hệ toạ độ Oxy, cho 4 điểm A(1;0),B(−2;4),C(−1;4),D(3;5). Tìm toạ độ điểm M thuộc đường thẳng (Δ):3x−y−5=0 sao cho hai tam giác MAB,MCD có diện tích bằng nhau.
Phương trình tham số của Δ:{x=ty=3t−5
Điểm M∈Δ⇒M(t;3t−5)
→AB(−3;4);→CD(4;1)
Phương trình đường thẳng AB:4x+3y−4=0
Phương trình đường thẳng CD:x−4y+17=0
SMAB=SMCD⇔d(M,AB).AB=d(M,CD).CD
|4t+3(3t−5)−4|√42+32.AB=|t−4(3t−5)+17|√1+42.CD⇒|13t−19|5.√42+32=|−11t+37|√17.√1+42
⇔t=−9∨t=73 ⇒M(−9;−32),M(73;2)
Trong mặt phẳng với hệ toạ độ Oxy, cho ΔABC có đỉnh A(1;2), phương trình đường trung tuyến BM:2x+y+1=0 và phân giác trong CD:x+y−1=0. Viết phương trình đường thẳng BC.
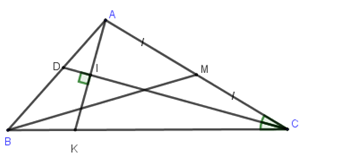
Điểm C∈CD:x+y−1=0⇒C(t;1−t).
Suy ra trung điểm M của AC là M(t+12;3−t2).
M thuộc BM nên (t+1)+3−t2+1=0⇒t=−7⇒C(−7;8)
Từ A(1;2), kẻ AI⊥CD(I∈CD) cắt BC tại K
Suy ra AK:(x−1)−(y−2)=0⇔x−y+1=0
Tọa độ điểm I thỏa hệ: {x+y−1=0x−y+1=0⇒I(0;1)
Tam giác ACK cân tại C nên I là trung điểm của AK⇒K(−1;0)
Đường thẳng BC đi qua C,K nên có phương trình:
x+1−7+1=y8⇔4x+3y+4=0
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có điểm I(6;2) là giao điểm của 2 đường chéo AC và BD. Điểm M(1;5) thuộc đường thẳng AB và trung điểm E của cạnh CD thuộc đường thẳng Δ:x+y−5=0. Viết phương trình đường thẳng AB.
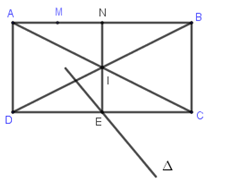
I(6;2);M(1;5)
Δ:x+y−5=0,E∈Δ⇒E(m;5−m);
Gọi N là trung điểm của AB
I trung điểm NE ⇒{xN=2xI−xE=12−myN=2yI−yE=4−5+m=m−1 ⇒N(12−m;m−1)
→MN=(11−m;m−6); →IE=(m−6;5−m−2)=(m−6;3−m)
→MN.→IE=0⇔(11−m)(m−6)+(m−6)(3−m)=0
⇔[m−6=014−2m=0 ⇔[m=6m=7
+ m=6⇒→MN=(5;0) nên phương trình AB là y=5
+ m=7⇒→MN=(4;1) nên phương trình AB là x−4y+19=0
Trong mặt phẳng với hệ toạ độ Oxy, cho tam giác ABC có phương trình đường phân giác trong góc A là d1:x+y+2=0, phương trình đường cao vẽ từ B là d2:2x−y+1=0, cạnh AB đi qua M(1;−1). Tìm phương trình cạnh AC.
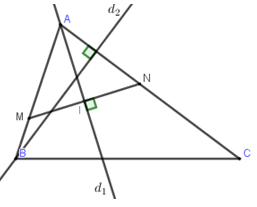
Gọi N là điểm đối xứng của M qua d1⇒N∈AC
→MN=(xN−1,yN+1)
Ta có: →MN cùng phương →nd1=(1;1)
⇔1(xN−1)−1(yN+1)=0⇔xN−yN=2(1)
Tọa độ trung điểm I của MN:xI=12(1+xN),yI=12(−1+yN)
I∈(d1)⇔12(1+xN)+12(−1+yN)+2=0⇔xN+yN+4=0(2)
Giải hệ (1) và (2) ta được N(−1;−3)
Phương trình cạnh AC vuông góc với d2 có dạng: x+2y+C=0.
N∈AC⇔−1+2.(−3)+C=0⇔C=7
Vậy, phương trình cạnh AC: x+2y+7=0.
Trong mặt phẳng với hệ trục tọa độ Oxy, cho đường thẳng (d):3x−4y−12=0. Phương trình đường thẳng (Δ) đi qua M(2;−1) và tạo với (d) một góc 45o có dạng ax+by+5=0, trong đó a,b cùng dấu. Khẳng định nào sau đây đúng?
Đường thẳng (d) có VTPT →n1=(3;−4)
Đường thẳng (Δ) có VTPT →n2=(a;b)
⇒cos(d;Δ)=cos(→n1;→n2)=|→n1.→n2||→n1|.|→n2|=|3a−4b|5√a2+b2⇔cos45o=|3a−4b|5√a2+b2⇔|3a−4b|5√a2+b2=√22⇔√2|3a−4b|=5√a2+b2⇔2(3a−4b)2=25(a2+b2)⇔7a2+48ab−7b2=0(1)
Mặt khác M(2;−1)∈Δ⇒2a−b+5=0⇔b=2a+5 thế vào (1)
⇒7a2+48a(2a+5)−7(2a+5)2=0⇔75a2+100a−175=0⇔[a=1⇒b=7(tm)a=−73⇒b=13(ktm)⇒a+b=8.Trong mặt phẳng với hệ trục tọa độ Oxy, cho hình chữ nhật có hai cạnh nằm trên đường thẳng có phương trình lần lượt là 2x−y+3=0; x+2y−5=0 và tọa độ một đỉnh là (2;3). Diện tích hình chữ nhật đó là:
Ta thấy d1:2x−y+3=0;d2:x+2y−5=0 là hai đường thẳng vuông góc.
Giả sử hình chữ nhật bài cho là ABCD có: AB:2x−y+3=0;AD:x+2y−5=0
Thay tọa độ điểm (2;3) vào các phương trình đường thẳng AB,AD ta thấy (2;3) không thuộc các đường thẳng trên ⇒C(2;3).
⇒SABCD=CB.CD=d(C;AB).d(C;AD)=|2.2−3+3|√22+12.|2+2.3−5|√12+22=4√5.3√5=125(dvdt)
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng đi qua hai điểm A(1;2), B(4;6), tìm tọa độ điểm M trên trục Oy sao cho diện tích ΔMAB bằng 1.
Gọi M(0;m)∈Oy;AB=√(4−1)2+(6−2)2=5.
Có SΔMAB=12d(M,AB).AB ⇔1=12.d(M,AB).5⇔d(M,AB)=25
→AB=(3;4)⇒→n=(4;−3) là 1 VTPT của AB.
⇒ Phương trình AB: 4(x−1)−3(y−2)=0⇔4x−3y+2=0
⇒d(M,AB)=|−3m+2|√42+32⇔25=|−3m+2|5⇔|−3m+2|=2
⇔[−3m+2=2−3m+2=−2⇔[m=0⇒M(0;0)m=43⇒M(0;43)
Khoảng cách từ điểm M (–2; 2) đến đường thẳng Δ: 5x - 12y + 8 = 0
d\left( {M;\Delta } \right) = \dfrac{{\left| { - 2.5 - 12.2 + 8} \right|}}{{\sqrt {{5^2} + {{12}^2}} }} = \dfrac{{26}}{{13}} = 2.
{\Delta _1}:\;\;3x + 4y = 12 \Leftrightarrow 3x + 4y - 12 = 0.
Xét phương trình đường thẳng {\Delta _1},\;{\Delta _2} ta có: \dfrac{3}{6} = \dfrac{4}{8} \ne - \dfrac{{12}}{{11}} \Rightarrow {\Delta _1}//{\Delta _2}.
Chọn A\left( {0;3} \right) \in {\Delta _1}. Khi đó ta có:
\Rightarrow d\left( {{\Delta _1};{\Delta _2}} \right) = d\left( {A;{\Delta _2}} \right) = \dfrac{{\left| {24 - 11} \right|}}{{\sqrt {{6^2} + {8^2}} }} = \dfrac{{13}}{{10}} = 1,3.
Gọi điểm I\left( {a;b} \right) thỏa mãn
2\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow 0 \Leftrightarrow 2\left( { - 1 - a;\;2 - b} \right) + \left( {3 - a;\;4 - b} \right) = \overrightarrow 0
\Rightarrow \left\{ \begin{array}{l}2\left( { - 1 - a} \right) + 3 - a = 0\\2\left( {2 - b} \right) + 4 - b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3a + 1 = 0\\ - 3b + 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{3}\\b = \dfrac{8}{3}\end{array} \right. \Rightarrow I\left( {\dfrac{1}{3};\dfrac{8}{3}} \right).
Ta có: 2A{M^2} + M{B^2} = 2{\left( {\overrightarrow {IM} - \overrightarrow {IA} } \right)^2} + {\left( {\overrightarrow {IB} - \overrightarrow {IM} } \right)^2}
\begin{array}{l} = 2\left( {I{M^2} - 2\overrightarrow {IM} .\overrightarrow {IA} + I{A^2}} \right) + I{B^2} - 2\overrightarrow {IB} .\overrightarrow {IM} + I{M^2}\\ = 3I{M^2} + 2I{A^2} + I{B^2} - 2\overrightarrow {IM} \left( {2\overrightarrow {IA} + \overrightarrow {IB} } \right) \\= 3I{M^2} + 2I{A^2} + I{B^2}\end{array}
2I{A^2} + I{B^2} không thay đổi nên 2A{M^2} + M{B^2} nhỏ nhất khi IM nhỏ nhất
\Leftrightarrow M là hình chiếu vuông góc của I lên \Delta
\Delta có VTPT là \overrightarrow n = \left( {1; - 2} \right)
Gọi d là đường thẳng đi qua I vuông góc với \Delta
\Rightarrow d nhận \overrightarrow {{n_1}} = \left( {2;\;1} \right) làm VTPT
\Rightarrow Phương trình tổng quát của d là: 2\left( {x - \dfrac{1}{3}} \right) + \left( {y - \dfrac{8}{3}} \right) = 0 \Leftrightarrow 2x + y - \dfrac{{10}}{3} = 0
M là giao điểm của d và \Delta \Rightarrow tọa độ điểm M là nghiệm của hệ phương trình:
\left\{ \begin{array}{l}2x + y - \dfrac{{10}}{3} = 0\\x - 2y - 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \dfrac{{26}}{{15}}\\y = - \dfrac{2}{{15}}\end{array} \right. \Rightarrow M\left( {\dfrac{{26}}{{15}}; - \dfrac{2}{{15}}} \right).
Vậy M\left( {\dfrac{{26}}{{15}}; - \dfrac{2}{{15}}} \right) thỏa mãn yêu cầu đề bài.
Trên mặt phẳng tọa độOxy, cho tam giác ABC có tọa độ các đỉnh là A\left( {2;3} \right),{\rm{ }}B\left( {5;0} \right) và C\left( { - 1;0} \right). Tìm tọa độ điểm M thuộc cạnh BC sao cho diện tích tam giác MAB bằng hai lần diện tích tam giác MAC
Phương trình đường thẳng BC là y = 0, vì M \in BC nên gọi M\left( {m;0} \right).
Ta có: \overrightarrow {AM} = \left( {m - 2; - 3} \right) nên \overrightarrow n = \left( {3;m - 2} \right) là 1 VTPT của đường thẳng AM.
Phương trình đường thẳng AM là:
\begin{array}{l}3\left( {x - 2} \right) + \left( {m - 2} \right)\left( {y - 3} \right) = 0\\ \Leftrightarrow 3x + \left( {m - 2} \right)y - 6 - 3m + 6 = 0\\ \Leftrightarrow 3x + \left( {m - 2} \right)y - 3m = 0\end{array}
\begin{array}{l} \Rightarrow d\left( {B;AM} \right) = \dfrac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\\\,\,\,\,\,\,d\left( {C;AM} \right) = \dfrac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\end{array}
Ta có: \left\{ \begin{array}{l}{S_{\Delta MAB}} = \dfrac{1}{2}d\left( {B;AM} \right).AM\\{S_{\Delta MAC}} = \dfrac{1}{2}d\left( {C;AM} \right).AM\end{array} \right. \Rightarrow {S_{\Delta MAB}} = 2{S_{\Delta MAC}} \Leftrightarrow d\left( {B;AM} \right) = 2d\left( {C;AM} \right).
\begin{array}{l} \Rightarrow \dfrac{{\left| {15 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }} = 2\dfrac{{\left| { - 3 - 3m} \right|}}{{\sqrt {9 + {{\left( {m - 2} \right)}^2}} }}\\ \Leftrightarrow \left| {15 - 3m} \right| = 2\left| { - 3 - 3m} \right|\\ \Leftrightarrow \left[ \begin{array}{l}15 - 3m = - 6 - 6m\\15 - 3m = 6 + 6m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 7\\m = 1\end{array} \right.\end{array}
Vậy M\left( {1;0} \right) hoặc M\left( { - 7;0} \right).

