Trong mặt phẳng tọa độ cho hình bình hành \(ABCD\) có \(A\left( {4;0} \right)\), phương trình đường trung tuyến kẻ từ \(B\) của tam giác \(ABC\) là \(7x + 4y - 5 = 0\) và phương trình đường trung trực của \(BC\) là \(2x + 8y - 5 = 0\). Biết hai điểm \(A,B\) nằm cùng phía so với đường trung trực của \(BC\). Tọa độ điểm \(B,C,D\) là

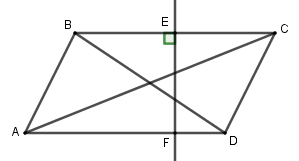
Từ hình vẽ: \(BD:7x + 4y - 5 = 0\), \(EF:2x + 8y - 5 = 0\).

Ta có : \(EF:2x + 8y - 5 = 0\) \( \Rightarrow \overrightarrow {{n_{EF}}}  = \left( {2;8} \right) \Rightarrow \overrightarrow {{u_{EF}}}  = \left( {8; - 2} \right)\).

Đường thẳng \(AD\) đi qua \(A\left( {4;0} \right)\) và vuông góc \(EF\) nên có VTPT \(\overrightarrow {{n_{AD}}}  = \dfrac{1}{2}\overrightarrow {{u_{EF}}}  = \left( {4; - 1} \right)\), khi đó

\(AD:4\left( {x - 4} \right) - \left( {y - 0} \right) = 0\) \( \Leftrightarrow 4x - y - 16 = 0\).

\(D = AD \cap BD\) nên tọa độ của \(D\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}7x + 4y - 5 = 0\\4x - y - 16 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y =  - 4\end{array} \right.\) hay \(D\left( {3; - 4} \right)\).

Dễ thấy \(BE = \dfrac{1}{2}AD\) \( = \dfrac{1}{2}\sqrt {{{\left( {3 - 4} \right)}^2} + {{\left( { - 4 - 0} \right)}^2}}  = \dfrac{{\sqrt {17} }}{2}\) hay \(d\left( {B,EF} \right) = \dfrac{{\sqrt {17} }}{2}\)

Gọi \(B\left( {t;\dfrac{{5 - 7t}}{4}} \right) \in BD\).

Khi đó \(d\left( {B,EF} \right) = \dfrac{{\sqrt {17} }}{2}\)\( \Leftrightarrow \dfrac{{\left| {2t + \dfrac{{8\left( {5 - 7t} \right)}}{4} - 5} \right|}}{{\sqrt {{2^2} + {8^2}} }} = \dfrac{{\sqrt {17} }}{2}\) \( \Leftrightarrow \dfrac{{\left| { - 12t + 5} \right|}}{{2\sqrt {17} }} = \dfrac{{\sqrt {17} }}{2} \Leftrightarrow \left| { - 12t + 5} \right| = 17\) \( \Leftrightarrow \left[ \begin{array}{l} - 12t + 5 = 17\\ - 12t + 5 =  - 17\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t =  - 1\\t = \dfrac{{11}}{6}\end{array} \right.\) \( \Rightarrow \left[ \begin{array}{l}B\left( { - 1;3} \right)\\B\left( {\dfrac{{11}}{6}; - \dfrac{{47}}{{24}}} \right)\end{array} \right.\).

Xét điểm \(B\left( { - 1;3} \right)\) ta thấy : \(\left( {2.4 + 8.0 - 5} \right)\left( {2.\left( { - 1} \right) + 8.3 - 5} \right) > 0\) nên \(A,B\) cùng phía so với \(EF\) (thỏa mãn).

Xét điểm \(B\left( {\dfrac{{11}}{6}; - \dfrac{{47}}{{24}}} \right)\) ta thấy : \(\left( {2.4 + 8.0 - 5} \right)\left( {2.\dfrac{{11}}{6} + 8.\left( { - \dfrac{{47}}{{24}}} \right) - 5} \right) < 0\) nên \(A,B\) khác phía so với \(EF\) (loại).

Do đó \(B\left( { - 1;3} \right)\).

Đường thẳng \(BC\) song song \(AD\) nên có phương trình dạng \(4x - y + c = 0\) với \(c \ne  - 16\).

\(B\left( { - 1;3} \right) \in BC\) nên \(4.\left( { - 1} \right) - 3 + c = 0 \Leftrightarrow c = 7\) hay \(BC:4x - y + 7 = 0\).

\(E = BC \cap EF\) nên tọa độ \(E\) thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}2x + 8y - 5 = 0\\4x - y + 7 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x =  - \dfrac{3}{2}\\y = 1\end{array} \right.\) \( \Rightarrow E\left( { - \dfrac{3}{2};1} \right)\).

\(E\) là trung điểm \(BC\) nên \(\left\{ \begin{array}{l}{x_C} = 2{x_E} - {x_B} =  - 2\\{y_C} = 2{y_E} - {y_B} =  - 1\end{array} \right.\) \( \Rightarrow C\left( { - 2; - 1} \right)\).

Vậy \(B\left( { - 1;3} \right),C\left( { - 2; - 1} \right),D\left( {3; - 4} \right)\).