Giá trị của \(E = \sin {36^0}\cos {6^0}-\sin {126^0}\cos {84^0}\) là
Ta có:
$E = \sin {36^0}\cos {6^0}$ $-\sin \left( {{{90}^0} + {{36}^0}} \right)\cos \left( {{{90}^0} - {6^0}} \right)$
$= \sin {36^0}\cos {6^0} - \cos {36^0}\sin {6^0}$
$= \sin \left( {{{36}^0} - {6^0}} \right) = \sin {30^0} = \dfrac{1}{2}$
Giá trị của biểu thức \(A = {\sin ^2}{51^0} + {\sin ^2}{55^0} + {\sin ^2}{39^0} + {\sin ^2}{35^0}\) là
\(\begin{array}{l}A = \left( {{{\sin }^2}{{51}^0} + {{\sin }^2}{{39}^0}} \right) + \left( {{{\sin }^2}{{55}^0} + {{\sin }^2}{{35}^0}} \right)\\ = \left( {{{\sin }^2}{{51}^0} + {{\cos }^2}{{51}^0}} \right) + \left( {{{\sin }^2}{{55}^0} + {{\cos }^2}{{55}^0}} \right) = 2\end{array}\)
Cho hai góc nhọn \(\alpha \) và \(\beta \) (\(\alpha < \beta )\). Khẳng định nào sau đây là sai?
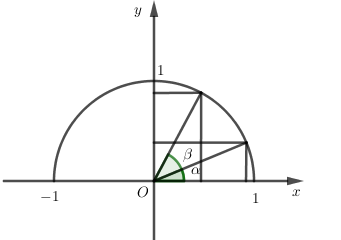
Vì \({0^0} < \alpha < \beta < {90^0}\) nên:
\(\begin{array}{l}0 < \sin \alpha < \sin \beta ,\cos \alpha > \cos \beta > 0\\0 < \tan \alpha < \tan \beta ,\cot \alpha > \cot \beta > 0\end{array}\)
Cho \(\Delta ABC\) vuông tại \(A\), góc \(B\) bằng \({30^0}\). Khẳng định nào sau đây là sai?
Ta có: \(\cos B = \cos {30^0} = \dfrac{{\sqrt 3 }}{2}\).
Cho biết \(\sin \alpha + \cos \alpha = a\). Giá trị của \(\sin \alpha .\cos \alpha \) bằng bao nhiêu?
Ta có:
\({a^2} = {\left( {\sin \alpha + \cos \alpha } \right)^2} = 1 + 2\sin \alpha \cos \alpha \Rightarrow \sin \alpha \cos \alpha = \dfrac{{{a^2} - 1}}{2}\).
Cho biết \(\cos \alpha = - \dfrac{2}{3}\) và \({90^0} < \alpha < {180^0}\). Tính \(\tan \alpha \)?
Do \({90^0} < \alpha < {180^0} \Rightarrow \tan \alpha < 0\).
Ta có: \(1 + {\tan ^2}\alpha = \dfrac{1}{{{{\cos }^2}\alpha }}\)\( \Leftrightarrow {\tan ^2}\alpha = \dfrac{5}{4}\)\( \Rightarrow \tan \alpha = - \dfrac{{\sqrt 5 }}{2}\).
Cho biết \(\cos \alpha = - \dfrac{2}{3}\). Tính giá trị của biểu thức \(E = \dfrac{{\cot \alpha + 3\tan \alpha }}{{2\cot \alpha + \tan \alpha }}\)?
\(E = \dfrac{{\cot \alpha + 3\tan \alpha }}{{2\cot \alpha + \tan \alpha }} \)\( = \dfrac{{1 + 3{{\tan }^2}\alpha }}{{2 + {{\tan }^2}\alpha }}\)\( = \dfrac{{3\left( {{{\tan }^2}\alpha + 1} \right) - 2}}{{1 + \left( {1 + {{\tan }^2}\alpha } \right)}}\)
\( = \dfrac{{\dfrac{3}{{{{\cos }^2}\alpha }} - 2}}{{\dfrac{1}{{{{\cos }^2}\alpha }} + 1}} \)\( = \dfrac{{3 - 2{{\cos }^2}\alpha }}{{1 + {{\cos }^2}\alpha }} = \dfrac{{19}}{{13}}\).
Cho biết \(\cot \alpha = 5\). Tính giá trị của \(E = 2{\cos ^2}\alpha + 5\sin \alpha \cos \alpha + 1\)?
Ta có:
$\begin{array}{l}
E = 2{\cos ^2}\alpha + 5\sin \alpha \cos \alpha + 1\\
= {\sin ^2}\alpha \left( {2.\frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} + 5.\frac{{\cos \alpha }}{{\sin \alpha }} + \frac{1}{{{{\sin }^2}\alpha }}} \right)\\
= \left( {\frac{1}{{{{\cot }^2}\alpha + 1}}} \right)\left( {2{{\cot }^2}\alpha + 5\cot \alpha + \frac{1}{{\frac{1}{{{{\cot }^2}\alpha + 1}}}}} \right)\\
= \left( {\frac{1}{{{{\cot }^2}\alpha + 1}}} \right)\left( {2{{\cot }^2}\alpha + 5\cot \alpha + {{\cot }^2}\alpha + 1} \right)\\
= \left( {\frac{1}{{{{\cot }^2}\alpha + 1}}} \right)\left( {3{{\cot }^2}\alpha + 5\cot \alpha + 1} \right)\\
= \frac{1}{{{5^2} + 1}}\left( {{{3.5}^2} + 5.5 + 1} \right) = \frac{{101}}{{26}}
\end{array}$
Trong các hệ thức sau hệ thức nào đúng?
Ta có: \({\sin ^2}2\alpha + {\cos ^2}2\alpha = 1\) nên D đúng.
Khẳng định nào sau đây là sai?
Ta có: \(\tan \alpha .\cot \alpha = 1\) nên C sai.
Giá trị của biểu thức \(A = \tan {1^0}\tan {2^0}\tan {3^0}...\tan {88^0}\tan {89^0}\) là
\(A = \left( {\tan {1^0}.\tan {{89}^0}} \right).\left( {\tan {2^0}.\tan {{88}^0}} \right)...\left( {\tan {{44}^0}.\tan {{46}^0}} \right).\tan {45^0} = 1\).
Rút gọn biểu thức sau \(A = \dfrac{{{{\cot }^2}x - {{\cos }^2}x}}{{{{\cot }^2}x}} + \dfrac{{\sin x.\cos x}}{{\cot x}}\).
\(A = \dfrac{{{{\cot }^2}x - {{\cos }^2}x}}{{{{\cot }^2}x}} + \dfrac{{\sin x.\cos x}}{{\cot x}} = 1 - \dfrac{{{{\cos }^2}x}}{{{{\cot }^2}x}} + \dfrac{{\sin x.\cos x}}{{\cot x}} = 1 - {\sin ^2}x + {\sin ^2}x = 1\).
Cho \(\tan \alpha + \cot \alpha = m\). Tìm \(m\) để \({\tan ^2}\alpha + {\cot ^2}\alpha = 7\).
\(7 = {\tan ^2}\alpha + {\cot ^2}\alpha = {\left( {\tan \alpha + \cot \alpha } \right)^2} - 2\)\( \Rightarrow {m^2} = 9\)\( \Leftrightarrow m = \pm 3\).
Cho \(\cot \alpha = \dfrac{1}{3}\). Giá trị của biểu thức \(A = \dfrac{{3\sin \alpha + 4\cos \alpha }}{{2\sin \alpha - 5\cos \alpha }}\) là:
Ta có: \(A = \dfrac{{3\sin \alpha + 4\sin \alpha .\cot \alpha }}{{2\sin \alpha - 5\sin \alpha .\cot \alpha }} = \dfrac{{3 + 4\cot \alpha }}{{2 - 5\cot \alpha }} = 13\).
Biết \(\sin a + \cos a = \sqrt 2 \). Hỏi giá trị của \({\sin ^4}a + {\cos ^4}a\) bằng bao nhiêu ?
Ta có: \(\sin a + \cos a = \sqrt 2 \)\( \Rightarrow 2 = {\left( {\sin a + \cos a} \right)^2}\) $ \Leftrightarrow 2 = {\sin ^2}a + 2\sin a\cos a + {\cos ^2}a $ $\Leftrightarrow 2 = 1 + 2\sin a\cos a \Leftrightarrow 1 = 2\sin a\cos a $ $\Leftrightarrow \sin a\cos a = \dfrac{1}{2}$
Do đó \({\sin ^4}a + {\cos ^4}a = \left( {{{\sin }^2}a + {{\cos }^2}a} \right) - 2{\sin ^2}a{\cos ^2}a \) \(= 1 - 2{\left( {\dfrac{1}{2}} \right)^2} = \dfrac{1}{2}\)
Biểu thức \(f\left( x \right) = 3\left( {{{\sin }^4}x + {{\cos }^4}x} \right) - 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right)\) có giá trị bằng:
\({\sin ^4}x + {\cos ^4}x ={\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 2{\sin ^2}x{\cos ^2}x\\= 1 - 2{\sin ^2}x{\cos ^2}x\)
\(\begin{array}{l}{\sin ^6}x + {\cos ^6}x = {\left( {{{\sin }^2}x} \right)^3} + {\left( {{{\cos }^2}x} \right)^3}\\ = \left( {{{\sin }^2}x + {{\cos }^2}x} \right)\left[ {{{\sin }^4}x - {{\sin }^2}x{{\cos }^2}x + {{\cos }^4}x} \right]\\ = {\sin ^4}x - {\sin ^2}x{\cos ^2}x + {\cos ^4}x\\ = {\sin ^4}x + 2{\sin ^2}x{\cos ^2}x + {\cos ^4}x - 3{\sin ^2}x{\cos ^2}x\\ = {\left( {{{\sin }^2}x + {{\cos }^2}x} \right)^2} - 3{\sin ^2}x{\cos ^2}x\\ = 1 - 3{\sin ^2}x{\cos ^2}x\end{array}\)
\(f\left( x \right) = 3\left( {1 - 2{{\sin }^2}x{{\cos }^2}x} \right) - 2\left( {1 - 3{{\sin }^2}x{{\cos }^2}x} \right) = 1\)

