Mệnh đề nào sau đây đúng?
Ta có: $\overrightarrow u = \left( {2; - 1} \right) = - \left( { - 2;1} \right) = - \overrightarrow v \,\,\,\,\, \Rightarrow \,\,\overrightarrow u $ và $\overrightarrow v $ đối nhau.
Khẳng định nào trong các khẳng định sau là đúng?
Ta có: $\overrightarrow a = \dfrac{5}{4}\overrightarrow b $ suy ra $\overrightarrow a $ cùng hướng với $\overrightarrow b $.
Cho $\overrightarrow a = \left( {x;2} \right),\overrightarrow b = \left( { - 5;1} \right),\overrightarrow c = \left( {x;7} \right)$. Vec tơ $\overrightarrow c = 2\overrightarrow a + 3\overrightarrow b $ nếu:
Ta có: $\overrightarrow c = 2\overrightarrow a + 3\overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}x = 2x + 3.\left( { - 5} \right)\\7 = 2.2 + 3.1\end{array} \right. \Leftrightarrow x = 15$.
Cho \(\overrightarrow a = (0,1)\),\(\overrightarrow b = ( - 1;2)\),\(\overrightarrow c = ( - 3; - 2)\). Tọa độ của \(\overrightarrow u = 3\overrightarrow a + 2\overrightarrow b - 4\overrightarrow c \)
Ta có: \(\overrightarrow u = 3\overrightarrow a + 2\overrightarrow b - 4\overrightarrow c = \left( {3.0 + 2.( - 1) - 4.( - 3);3.1 + 2.2 - 4.( - 2)} \right) = \left( {10;15} \right)\).
Cho\(A\left( {0;3} \right),\,B\left( {4;2} \right)\). Điểm \(D\) thỏa $\overrightarrow {OD} + 2\overrightarrow {DA} - 2\overrightarrow {DB} = \overrightarrow 0 $, tọa độ\(D\) là:
Ta có: $\overrightarrow {OD} + 2\overrightarrow {DA} - 2\overrightarrow {DB} = \overrightarrow 0 \Leftrightarrow \left\{ \begin{array}{l}{x_D} - 0 + 2\left( {0 - {x_D}} \right) - 2\left( {4 - {x_D}} \right) = 0\\{y_D} - 0 + 2\left( {3 - {y_D}} \right) - 2\left( {2 - {y_D}} \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 8\\{y_D} = - 2\end{array} \right.$.
Cho $\overrightarrow a = 3\overrightarrow i - 4\overrightarrow j $ và $\overrightarrow b = \overrightarrow i - \overrightarrow j $. Tìm phát biểu sai:
Ta có: $\overrightarrow a = 3\overrightarrow i - 4\overrightarrow j \Rightarrow \overrightarrow a \left( {3; - 4} \right)$ $ \Rightarrow \left| {\overrightarrow a } \right| = \sqrt {{3^2} + {{\left( { - 4} \right)}^2}} = 5$ nên A đúng.
$\overrightarrow b = \overrightarrow i - \overrightarrow j \Rightarrow \overrightarrow b \left( {1; - 1} \right) $ $\Rightarrow \left| {\overrightarrow b } \right| = \sqrt {{1^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 $ nên D đúng, B sai.
Ngoài ra $\overrightarrow a - \overrightarrow b = \left( {2; - 3} \right)$ nên C đúng.
Cho $A\left( {1;2} \right),\,B\left( { - 2;6} \right)$. Điểm $M$ trên trục $Oy$ sao cho ba điểm $A,B,M$ thẳng hàng thì tọa độ điểm $M$ là:
Ta có: $M$ trên trục $Oy \Rightarrow M\left( {0;y} \right)$
Ba điểm $A,B,M$ thẳng hàng khi $\overrightarrow {AB} $ cùng phương với $\overrightarrow {AM} $
Ta có $\overrightarrow {AB} = \left( { - 3;4} \right),\,\,\overrightarrow {AM} = \left( { - 1;y - 2} \right)$.
Do đó, $\overrightarrow {AB} $ cùng phương với $\overrightarrow {AM} \Leftrightarrow \dfrac{{ - 1}}{{ - 3}} = \dfrac{{y - 2}}{4} \Rightarrow y = \dfrac{{10}}{3}$.
Vậy $M\left( {0;\dfrac{{10}}{3}} \right)$
Trong hệ tọa độ \(Oxy,\) cho hình chữ nhật \(ABCD\) có \(A\left( {0;3} \right)\), \(D\left( {2;1} \right)\) và \(I\left( { - 1;0} \right)\) là tâm của hình chữ nhật. Tìm tọa độ trung điểm của cạnh \(BC.\)
Gọi \(M\) là tọa độ trung điểm của cạnh \(AD\)\( \Rightarrow M\left( {1;2} \right)\)
Gọi \(N\left( {{x_N};{y_N}} \right)\) là tọa độ trung điểm của cạnh \(BC.\)
Do \(I\) là tâm của hình chữ nhật \( \Rightarrow I\) là trung điểm của \(MN\).
Suy ra \(\left\{ \begin{array}{l}{x_N} = 2{x_I} - {x_M} = - 3\\{y_N} = 2{y_I} - {y_M} = - 2\end{array} \right.\) \( \Rightarrow N\left( { - 3; - 2} \right)\)
Trong mặt phẳng $Oxy$, cho các điểm $A\left( { - 3;3} \right),B\left( {1;4} \right),C\left( {2; - 5} \right)$. Tọa độ điểm $M$ thỏa mãn $2\overrightarrow {MA} - \overrightarrow {BC} = 4\overrightarrow {CM} $ là:
Ta có: $2\overrightarrow {MA} - \overrightarrow {BC} = 4\overrightarrow {CM} \Leftrightarrow \left\{ \begin{array}{l}2\left( { - 3 - {x_M}} \right) - \left( {2 - 1} \right) = 4\left( {{x_M} - 2} \right)\\2\left( {3 - {y_M}} \right) - \left( { - 5 - 4} \right) = 4\left( {{y_M} + 5} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = \dfrac{1}{6}\\{y_M} = - \dfrac{5}{6}\end{array} \right. \Rightarrow M\left( {\dfrac{1}{6}; - \dfrac{5}{6}} \right)$.
Trong mặt phẳng tọa độ \(Oxy\) cho bốn điểm \(A\left( {3; - 2} \right),\;B\left( {7;1} \right),\;C\left( {0;1} \right),\;D\left( { - 8; - 5} \right)\). Khẳng định nào sau đây là đúng?
Ta có: \(\overrightarrow {AB} = \left( {4;3} \right),\,\overrightarrow {CD} = \left( { - 8; - 6} \right) \Rightarrow \overrightarrow {CD} = - 2\overrightarrow {AB} \).
Trong mặt phẳng $Oxy$, cho $A\left( { - 2;0} \right),\;B\left( {5; - 4} \right),\;C\left( { - 5;1} \right)$. Tọa độ điểm $D$ để tứ giác $BCAD$ là hình bình hành là:
Ta có: tứ giác $BCAD$ là hình bình hành khi $\overrightarrow {BC} = \overrightarrow {DA} \Leftrightarrow \left\{ \begin{array}{l} - 5 - 5 = - 2 - {x_D}\\1 + 4 = 0 - {y_D}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 8\\{y_D} = - 5\end{array} \right.$.
Cho \(M\left( {2;0} \right),\,N\left( {2;2} \right),\,P\left( { - 1;3} \right)\) lần lượt là trung điểm các cạnh \(BC,\,CA,\,AB\) của \(\Delta ABC\). Tọa độ \(B\) là:
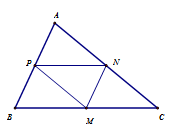
Ta có: $BPNM$ là hình bình hành nên $\left\{ \begin{array}{l}{x_B} + {x_N} = {x_P} + {x_M}\\{y_B} + {y_N} = {y_P} + {y_M}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + 2 = 2 + ( - 1)\\{y_B} + 2 = 0 + 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} = - 1\\{y_B} = 1\end{array} \right.$.
Trong mặt phẳng tọa độ \(Oxy\) cho \(\overrightarrow a = (2;1),\overrightarrow {{\rm{ }}b} = (3;4),{\rm{ }}\overrightarrow c = (7;2)\). Cho biết \(\overrightarrow c = m.\overrightarrow a + n.\overrightarrow b \). Khi đó
Ta có: \(\overrightarrow c = m.\overrightarrow a + n.\overrightarrow b \Leftrightarrow \left\{ \begin{array}{l}7 = 2m + 3n\\2 = m + 4n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = \dfrac{{22}}{5}\\n = - \dfrac{3}{5}\end{array} \right.\).
Cho các vectơ $\overrightarrow a = \left( {4; - 2} \right),\overrightarrow b = \left( { - 1; - 1} \right),\overrightarrow c = \left( {2;5} \right)$. Phân tích vectơ $\overrightarrow b $ theo hai vectơ $\overrightarrow a {\rm{ và }}\overrightarrow c $, ta được:
Giả sử $\overrightarrow b = m\overrightarrow a + n\overrightarrow c \Leftrightarrow \left\{ \begin{array}{l} - 1 = 4m + 2n\\ - 1 = - 2m + 5n\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = - \dfrac{1}{8}\\n = - \dfrac{1}{4}\end{array} \right.$
Vậy $\overrightarrow b = - \dfrac{1}{8}\overrightarrow a - \dfrac{1}{4}\overrightarrow c $.
Trong mặt phẳng $Oxy$, cho $A\left( {m - 1; - 1} \right),\,B\left( {2;2 - 2m} \right),\,C\left( {m + 3;3} \right)$. Tìm giá trị $m$ để $A,B,C$ là ba điểm thẳng hàng?
Ta có: $\overrightarrow {AB} = \left( {3 - m;3 - 2m} \right)$, $\overrightarrow {AC} = \left( {4;4} \right)$
Ba điểm $A,B,C$ thẳng hàng khi và chỉ khi $\overrightarrow {AB} $ cùng phương với $\overrightarrow {AC} $
$ \Leftrightarrow \dfrac{{3 - m}}{4} = \dfrac{{3 - 2m}}{4} \Leftrightarrow m = 0$.
Cho các điểm \(A\left( { - 2;1} \right),\,B\left( {4;0} \right),\,C\left( {2;3} \right)\). Tìm điểm \(M\) biết rằng \(\overrightarrow {CM} + 3\overrightarrow {AC} = 2\overrightarrow {AB} \)
Gọi \(M\left( {{x_M};{y_M}} \right)\). Ta có:
\(\overrightarrow {CM} + 3\overrightarrow {AC} = 2\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}{x_M} - 2 + 3\left( {2 + 2} \right) = 2\left( {4 + 2} \right)\\{y_M} - 3 + 3\left( {3 - 1} \right) = 2\left( {0 - 1} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 2\\{y_M} = - 5\end{array} \right. \Rightarrow M\left( {2; - 5} \right)\)

