Nhân ngày Quốc tế Thiếu nhi 1-6, một rạp chiếu phim phục vụ các khán giả một bộ phim hoạt hình. Vé được bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6-13 tuổi): 50 000 đồng/vé
Loại 2 (dành cho người trên 13 tuổi): 100 000 đồng/vé.
Người ta tính toán rằng, để không phải bù lỗ thì số tiền về thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng.
Gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được.
Viết biểu thức tính số tiền bán vé thu được (đơn vị nghìn đồng) ở rạp chiếu phim đó theo x và y.
Bước 1:
Số tiền bán x vé loại 1 là: \(x.50000\) (đồng)
Số tiền bán y vé loại 2 là: \(y.100000\) (đồng)
Bước 2:
Số tiền thu được là
\(50000x + 100000y\) (đồng)
Nhân ngày Quốc tế Thiếu nhi 1-6, một rạp chiếu phim phục vụ các khán giả một bộ phim hoạt hình. Vé được bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6-13 tuổi): 50 000 đồng/vé
Loại 2 (dành cho người trên 13 tuổi): 100 000 đồng/vé.
Người ta tính toán rằng, để không phải bù lỗ thì số tiền về thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng.
Gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được.
Các số nguyên không âm x và y phải thoả mãn điều kiện gì để số tiền bán vé thu được đạt tối thiểu 20 triệu đồng?
Ta có 20 triệu = 20 000 000=\({2.10^7}\) (đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50000x + 100000y\) (đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50000x + 100000y \ge {2.10^7}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Nhân ngày Quốc tế Thiếu nhi 1-6, một rạp chiếu phim phục vụ các khán giả một bộ phim hoạt hình. Vé được bán ra có hai loại:
Loại 1 (dành cho trẻ từ 6-13 tuổi): 50 000 đồng/vé
Loại 2 (dành cho người trên 13 tuổi): 100 000 đồng/vé.
Người ta tính toán rằng, để không phải bù lỗ thì số tiền về thu được ở rạp chiếu phim này phải đạt tối thiểu 20 triệu đồng.
Gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được.
Nếu số tiền bán vé thu được nhỏ hơn 20 triệu đồng thì x và y thỏa mãn điều kiện gì?
Ta có 20 triệu = 20 000 000=\({2.10^7}\) (đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50000x + 100000y\) (đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50000x + 100000y < {2.10^7}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Cặp số nào sau đây là nghiệm của bất phương trình \(2x - 3y < 3\)?
\(\left( {2;1} \right)\)
\(\left( {2;1} \right)\)
\(\left( {2;1} \right)\)
+ Thay \(x = 0,y = - 1\)vào bất phương trình \(2x - 3y < 3\) ta được:
\(2.0 - 3.\left( { - 1} \right) < 3 \Leftrightarrow 3 < 3\) (Vô lý)
Vậy \(\left( {0; - 1} \right)\) không là nghiệm.
+ Thay \(x = 2,y = 1\)vào bất phương trình \(2x - 3y < 3\) ta được:
\(2.2 - 3.1 < 3 \Leftrightarrow 1 < 3\) (Luôn đúng)
Vậy \(\left( {2;1} \right)\) là nghiệm.
+ Thay \(x = 3,y = 1\)vào bất phương trình \(2x - 3y < 3\) ta được:
\(2.3 - 3.1 < 3 \Leftrightarrow 3 < 3\) (Vô lý)
Vậy \(\left( {3;1} \right)\) không là nghiệm.
Phần không gạch (không kể d) hình sau là miền nghiệm của bất phương trình nào?

Đường thẳng qua điểm (2;0) và (0;1) nên phương trình đường thẳng là
Thay x=2, y=0 vào phương trình \(y = ax + b\) ta được \(0 = 2a + b\)
Thay x=0, y=1 vào phương trình \(y = ax + b\) ta được \(1 = 0.a + b\)
=> \(a = - \dfrac{1}{2},b = 1\)
=> phương trình đường thẳng là \(y = - \dfrac{1}{2}x + 1\)
Lấy điểm (3;0) thuộc miền nghiệm ta có \( - \dfrac{1}{2}x + 1 - y = \dfrac{{ - 1}}{2} < 0\)
=> Bất phương trình cần tìm là \( - \dfrac{1}{2}x - y + 1 \le 0\)
Một gian hàng trưng bày bàn và ghế rộng 60 \({m^2}\). Diện tích để kê một chiếc ghế là 0,5\({m^2}\), một chiếc bàn là 1,2 \({m^2}\). Gọi x là số chiếc ghế, y là số chiếc bàn được kê.
Viết bất phương trình bậc nhất hai ẩn x, y cho phần mặt sàn để kê bàn và ghế, biết diện tích mặt sàn dành cho lưu thông tối thiểu là 12 \({m^2}\).
Bước 1: Biểu diễn diện tích x chiếc ghế và y chiếc bàn.
Diện tích của x chiếc ghế là \(0,5x\left( {{m^2}} \right)\) và y chiếc bàn là \(1,2y\left( {{m^2}} \right)\)
Bước 2: Biểu diễn diện tích lưu thông và cho lớn hơn hoặc bằng 12 \({m^2}\).
Tổng diện tích x chiếc ghế và y chiếc bàn là \(0,5x + 1,2y\left( {{m^2}} \right)\)
Diện tích lưu thông là \(60 - 0,5x - 1,2y\left( {{m^2}} \right)\)
Bất phương trình cần tìm là
\(\begin{array}{l}60 - 0,5x - 1,2y \ge 12\\ \Leftrightarrow 0,5x + 1,2y \le 48\end{array}\)
Một gian hàng trưng bày bàn và ghế rộng 60 \({m^2}\). Diện tích để kê một chiếc ghế là 0,5\({m^2}\), một chiếc bàn là 1,2 \({m^2}\). Gọi x là số chiếc ghế, y là số chiếc bàn được kê.
Trong các cặp số (10;10), (10;20) và (20;10), có bao nhiêu cặp là nghiệm của bất phương đã lập được?
+) Thay x=10, y=10 ta được
=> (10;10) là nghiệm của bất phương trình
+) Thay x=10, y=20 ta được
=> (10;20) là nghiệm của bất phương trình
+) Thay x=20, y=10 ta được
=> (20;10) là nghiệm của bất phương trình.
Vậy cả 3 cặp số là nghiệm của bất phương trình.
Cho hệ bất phương trình sau:
\(\left\{ \begin{array}{l}x - y < 3\left( 1 \right)\\x + 2y > - 2\left( 2 \right)\end{array} \right.\)
Cặp số là nghiệm của bất phương trình đã cho là:
(1;1)
(1;1)
(1;1)
+ Thay x=1;y=1 vào (1) ta được: 1-1<3(Luôn đúng)
Thay x=1; y=1 vào (2) ta được: 1+2.1>-2(Luôn đúng)
Vậy cặp số (1;1) là nghiệm của hệ bất phương trình đã cho.
+ Thay x=-5;y=1 vào (1) ta được: -5-1<3(Luôn đúng)
Thay x=-5; y=1 vào (2) ta được: -5+2.1>-2(Sai)
Vậy cặp số (-5;1) là không nghiệm của hệ bất phương trình đã cho.
Miền không bị gạch ở hình sau là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
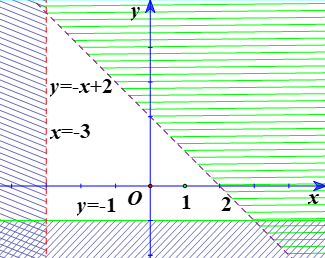
\(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\)
\(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\)
\(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\)
Ta thấy các đường thẳng trên hình là \(y = - 1;x = - 3;x + y = - 2\)
Từ các phương trình trên thì ta chọn luôn hệ thứ nhất mà không cần xét tiếp.

