Câu hỏi:
2 năm trước
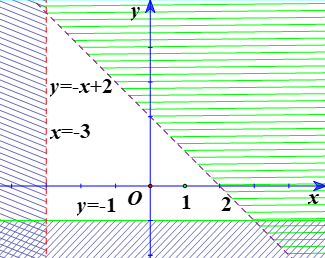
Miền không bị gạch ở hình sau là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?
Trả lời bởi giáo viên
Đáp án đúng:
\(\left\{ \begin{array}{l}x + y < 2\\x > - 3\\y \ge - 1\end{array} \right.\)
Ta thấy các đường thẳng trên hình là \(y = - 1;x = - 3;x + y = - 2\)
Từ các phương trình trên thì ta chọn luôn hệ thứ nhất mà không cần xét tiếp.
Hướng dẫn giải:
Xác định các đường thẳng dạng trên mỗi hình.
Với các đường thẳng x=a, nếu phần không bị gạch bên phải thì bất phương trình tương ứng là \(x < a\) hoặc \(x \le a\), ngược lại sẽ là \(x > a\) hoặc \(x \ge a\).
Với các đường thẳng y=b, nếu phần không bị gạch bên trên thì bất phương trình là \(y > b\) hoặc \(y \ge b\), ngược lại sẽ là \(y < b\) hoặc \(y \le b\).
Với các đường thẳng \(y = ax + b\) cắt hai trục thì thay tọa độ điểm thuộc miền nghiệm vào, nếu vế trái nhỏ hơn vế phải thì bất phương trình là \(y < ax + b\) hoặc \(y \le ax + b\), ngược lại thì bất phương trình là \(y > ax + b\) hoặc \(y \ge ax + b\).
Câu hỏi khác
- Bài tập bất phương trình và hệ bất phương trình bậc nhất hai ẩn toán 10 có lời giải
- Bài tập bất phương trình và hệ bất phương trình bậc nhất một ẩn toán 10 có lời giải
- Bài tập bất đẳng thức toán 10 có lời giải
- Bài tập dấu của nhị thức bậc nhất toán 10 có lời giải
- Bài tập đại cương về bất phương trình toán 10 có lời giải
