Cho tam giác ABC có trung tuyến AM. Chọn khẳng định đúng
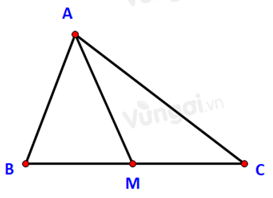
Ta có: \( \widehat {AMB} + \widehat {AMC} = {180^o}\)
\( \Rightarrow \cos \widehat {AMB} = - \cos \widehat {AMC}\)
Hay \( \cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
Tính giá trị của các biểu thức sau:
\( M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
\( M = \sin {45^o}.\cos {45^o} + \sin {30^o}\)
Ta có: \( \left\{ \begin{array}{l}\sin {45^o} = \cos {45^o} = \dfrac{{\sqrt 2 }}{2};\;\\\sin {30^o} = \dfrac{1}{2}\end{array} \right.\)
Thay vào M, ta được: \( M = \dfrac{{\sqrt 2 }}{2}.\dfrac{{\sqrt 2 }}{2} + \dfrac{1}{2} = \dfrac{2}{4} + \dfrac{1}{2} = 1\)
Điền dấu ">,<,=" vào chỗ trống:
Cho tam giác ABC.
Nếu góc A nhọn thì \( {b^2} + {c^2}\)
\( {a^2}\)
Cho tam giác ABC.
Nếu góc A nhọn thì \( {b^2} + {c^2}\)
\( {a^2}\)
Theo định lí cos ta có: \( {a^2} = {b^2} + {c^2} - 2bc\;\cos A\)
\( \Rightarrow {b^2} + {c^2} - {a^2} = 2bc\;\cos A\)(1)
Mặt khác, xét nửa đường tròn đường giác:
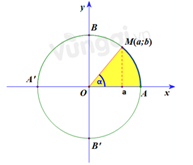
Ta có: \( \cos \alpha = a\) với a là hoành độ của điểm M.
Dễ dàng suy ra:
Nếu góc A nhọn thì \( \cos A > 0\)
Từ (1), suy ra \( {b^2} + {c^2} - {a^2} = 2bc\;\cos A > 0\)
Hay \( {b^2} + {c^2} > {a^2}\)

