Cho hypebol $(H):\,4{x^2} - {y^2} = 4$, độ dài của trục thực và trục ảo của $(H)$ lần lượt là:
$(H):\,4{x^2} - {y^2} = 4 \Leftrightarrow \dfrac{{{x^2}}}{1} - \dfrac{{{y^2}}}{4} = 1 \Rightarrow a = 1;b = 2$
Độ dài trục thực: ${A_1}{A_2} = 2a = 2.1 = 2$
Độ dài trục ảo: ${B_1}{B_2} = 2b = 2.2 = 4$.
Hypebol $(H):\,\,16{x^2} - 9{y^2} = 16$ có các đường tiệm cận là:
$(H):\,\,16{x^2} - 9{y^2} = 16 \Leftrightarrow \dfrac{{{x^2}}}{1} - \dfrac{{{y^2}}}{{\dfrac{{16}}{9}}} = 1 \Rightarrow a = 1,\,\,b = \dfrac{4}{3}$
Hai đường tiệm cận của $(H)$: $y = \dfrac{b}{a}x = \dfrac{{\dfrac{4}{3}}}{1}x = \dfrac{4}{3}x;\,\,y = - \dfrac{b}{a}x = - \dfrac{{\dfrac{4}{3}}}{1}x = - \dfrac{4}{3}x$.
Lập phương trình chính tắc của hypebol $(H)$ biết $(H)$ có trục thực, trục ảo dài lần lượt là 10 và 6.
$(H)$ có trục thực, trục ảo dài lần lượt là 10 và 6 $ \Rightarrow a = 5,\,\,b = 3$.
Phương trình chính tắc của $(H)$: $\dfrac{{{x^2}}}{{25}} - \dfrac{{{y^2}}}{9} = 1$.
Trong mặt phẳng tọa độ Oxy cho tam giác ABC có hình chiếu của C trên đường thẳng AB là \(H\left( { - 1; - 1} \right)\), đường thẳng chứa phân giác của góc A có phương trình x – y + 2 = 0 và đường cao kẻ từ B có phương trình 4x + 3y – 1 = 0. Tìm tọa độ điểm C.
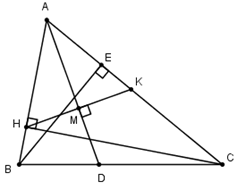
Gọi K là điểm đối xứng với H qua đường phân giác AD: x – y + 2 = 0 \( \Rightarrow \) đường thẳng HK có phương trình x + y + 2 = 0. Tọa độ giao điểm của HK với d là nghiệm của hệ:
\(\left\{ \begin{array}{l}x - y + 2 = 0\\x + y + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 2\\y = 0\end{array} \right. \Leftrightarrow M\left( { - 2;0} \right)\) là trung điểm của HK
\( \Rightarrow \left\{ \begin{array}{l}{x_K} = 2{x_M} - {x_H} = - 4 + 1 = - 3\\{y_K} = 2{y_M} - {y_H} = 0 + 1 = 1\end{array} \right. \Rightarrow K\left( { - 3;1} \right)\)
Đường thẳng \(AC \bot BE:4x + 3y - 1 = 0\) và đi qua K nên AC có phương trình \(3\left( {x + 3} \right) - 4\left( {y - 1} \right) = 0 \Leftrightarrow 3x - 4y + 13 = 0\)
Đỉnh \(A = AC \cap AD \Rightarrow \) Tọa độ của A là nghiệm của hệ \(\left\{ \begin{array}{l}x - y + 2 = 0\\3x - 4y + 13 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 7\end{array} \right. \Rightarrow A\left( {5;7} \right)\)
Đường thẳng CH đi qua \(H\left( { - 1; - 1} \right)\) và có vector pháp tuyến \(\dfrac{1}{2}\overrightarrow {AH} = \dfrac{1}{2}\left( {6;8} \right) = \left( {3;4} \right)\) , do đó có phương trình \(3\left( {x + 1} \right) + 4\left( {y + 1} \right) = 0 \Leftrightarrow 3x + 4y + 7 = 0\)
Đỉnh \(C = CH \cap AC \Rightarrow \) Tọa độ của C là nghiệm của hệ \(\left\{ \begin{array}{l}3x + 4y + 7 = 0\\3x - 4y + 13 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \dfrac{{10}}{3}\\y = \dfrac{3}{4}\end{array} \right. \Rightarrow C\left( { - \dfrac{{10}}{3};\dfrac{3}{4}} \right)\)
Cho hai điểm \(A(3;0),B(0;4)\). Phương trình đường tròn (C) có bán kính nhỏ nhất nội tiếp tam giác OAB là:
Phương trình đường thẳng AB là: \(\dfrac{x}{3} + \dfrac{y}{4} = 1 \Leftrightarrow 4x + 3y - 12 = 0\)
Giả sử đường tròn (C) có tâm \(I\left( {a,b} \right)\).
Đường tròn (C) nội tiếp tam giác OAB, suy ra \(\left( C \right)\)có bán kính nhỏ nhất và tiếp xúc \({\rm{Ox}},Oy,AB\)
\( \Rightarrow R = d\left( {I,{\rm{Ox}}} \right) = d\left( {I,Oy} \right) = d(I,AB)\)
\( \Rightarrow R = \left| b \right| = \left| a \right| = \dfrac{{\left| {4a + 3b - 12} \right|}}{5}\)
TH1: Nếu \(a = b\), ta có $\left| a \right| = \dfrac{{\left| {4a + 3a - 12} \right|}}{5} \Leftrightarrow 5\left| a \right| = \left| {7a - 12} \right|$ $ \Leftrightarrow \left[ \begin{array}{l}5a = 7a - 12\\5a = 12 - 7a\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = 6\\a = 1\end{array} \right.$
TH2: Nếu \( - a = b\), ta có $\left| a \right| = \dfrac{{\left| {4a - 3a - 12} \right|}}{5} \Leftrightarrow 5\left| a \right| = \left| {a - 12} \right|$ $ \Leftrightarrow \left[ \begin{array}{l}5a = a - 12\\5a = 12 - a\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = - 3\\a = 2\end{array} \right.$
Vì $\left( C \right)$ có bán kính nhỏ nhất nên chọn \(R = \left| a \right| = 1\).
Suy ra $\left( C \right)$ có tâm \(I(1;1)\) và $R = 1$\( \Rightarrow \left( C \right):{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 1\)\( \Leftrightarrow {x^2} + {y^2} - 2x - 2y + 1 = 0\)
Cho đường thẳng \(d:x - 2y + 2 = 0\) và hai điểm \(A\left( {0;6} \right),B\left( {2;5} \right).\) Điểm \(M\left( {a;b} \right)\) nằm trên đường thẳng \(d\) thỏa mãn \(M{A^2} + M{B^2}\) đạt giá trị nhỏ nhất. Tính giá trị \(P = a + b.\)
Ta có \(M \in d:\,\,\,x - 2y + 2 = 0 \Rightarrow M\left( {a;\dfrac{{a + 2}}{2}} \right).\)
Khi đó: \(M{A^2} + M{B^2} = \left[ {{{\left( { - a} \right)}^2} + {{\left( {6 - \dfrac{{a + 2}}{2}} \right)}^2}} \right] + \left[ {{{\left( {2 - a} \right)}^2} + {{\left( {5 - \dfrac{{a + 2}}{2}} \right)}^2}} \right]\)
\(\begin{array}{l} \Rightarrow M{A^2} + M{B^2} = {a^2} + \dfrac{{{{\left( {10 - a} \right)}^2}}}{4} + {a^2} - 4a + 4 + \dfrac{{{{\left( {8 - a} \right)}^2}}}{4}\\ = 2{a^2} - 4a + 4 + \dfrac{{{a^2}}}{2} - 9a + 41\\ = \dfrac{5}{2}{a^2} - 13a + 45 = \dfrac{5}{2}\left( {{a^2} - \dfrac{{26}}{5}a} \right) + 45\\ = \dfrac{5}{2}{\left( {a - \dfrac{{13}}{5}} \right)^2} + \dfrac{{281}}{{10}} \ge \dfrac{{281}}{{10}}.\end{array}\)
Dấu “=” xảy ra \( \Leftrightarrow a - \dfrac{{13}}{5} = 0 \Leftrightarrow a = \dfrac{{13}}{5}\) \( \Rightarrow b = \dfrac{{\dfrac{{13}}{5} + 2}}{2} = \dfrac{{23}}{{10}}\)
\( \Rightarrow a + b = \dfrac{{13}}{5} + \dfrac{{23}}{{10}} = \dfrac{{49}}{{10}}.\)

