Cho hai tia Ax và By nằm trên hai đường thẳng chéo nhau. Một điểm M chạy trên Ax và một điểm N chạy trên By sao cho AM = kBN (k > 0 cho trước)
LG a
Chứng minh rằng MN song song với một mặt phẳng cố định
Giải chi tiết:
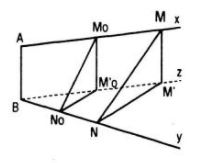
Dựng tia Bz song song và cùng hướng với tia Ax. Trên các tia Ax, By và Bz lần lượt lấy các điểm cố định M0, N0 và M’0 sao cho \({{A{M_0}} \over {B{N_0}}} = k\) và \(BM{'_0} = A{M_0}\)
Khi đó ta có : \({M_0}M{'_0}//AB\) và \({{BM{'_0}} \over {BN_0}} = k\,\,\left( 1 \right)\)
Lấy điểm M’ thuộc tia Bz sao cho BM’ = AM.
Từ (1) và (2) ta có : MM’ // M0M’0 (3)
Và \({{BM'} \over {BN}} = {{B{M'_0}} \over {B{N_0}}}\,\,\left( 4 \right)\)
Từ (4) suy ra NM’ // N0M’0 (5)
Từ (3) và (5) suy ra mp(MNM’) // mp(M0N0M’0).
Vậy MN luôn song song với mặt phẳng cố định (M0N0M’0)
LG b
Tìm tập hợp các điểm I thuộc đoạn MN sao cho IM = kIN
Giải chi tiết:
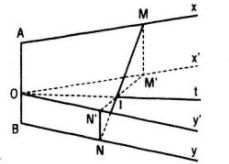
Thuận. Gọi O là một điểm thuộc đoạn thẳng AB sao cho OA : OB = k. Từ O ta vẽ hai tia Ox’ và Oy’ sao cho Ox’ // Ax, Oy’ // By. Xét phép chiếu song song theo phương AB lên mp(Ox’, Oy’). Gọi M’, N’ lần lượt là hình chiếu của M và N theo phép chiếu này. Khi đó, giao điểm của MN và M’N’ chính là điểm I vì rõ ràng ta có :
\({{IM} \over {IN}} = {{M'M} \over {N'N}} = {{OA} \over {OB}} = k\)
Trong tam giác M’ON’, ta có : \({{IM'} \over {IN'}} = k,{{OM'} \over {ON'}} = {{AM} \over {BN}} = k\)
Vậy \({{IM'} \over {IN'}} = {{OM'} \over {ON'}} = k.\) Từ đó suy ra I phải nằm trên tia phân giác Ot của góc x’Oy’.
Đảo. Giả sử I là một điểm bất kì thuộc tia phân giác Ot của góc x’Oy’.
Gọi M’, N’ là những điểm lần lượt thuộc tia Ox’, tia Oy’ sao cho M’, I, N’ thẳng hàng và \({{IM'} \over {IN'}} = k\) (có thể tìm M’, N’ bằng cách dùng phép vị tự tâm I tỉ số -k trên mp(Ox’y’)). Gọi M, N lần lượt là những điểm thuộc các tia Ax, By sao cho AM = OM’, BN = ON’. Dễ thấy I, M, N thẳng hàng và IM : IN = k
Kết luận : Tập hợp các điểm I thỏa mãn điều kiện bài toán là tia phân giác Ot của góc x’Oy’.

