Một vật nặng treo bởi một chiếc lò xo, chuyển động lên xuống qua vị trí cân bằng.
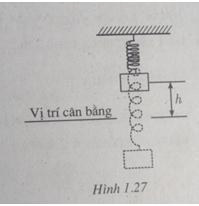
Khoảng cách \(h\) từ vật đó đến vị trí cân bằng ở thời điểm \(t\) giây được tính theo công thức \(h = |d|\) trong đó
\(d = 5\sin6t – 4\cos6t\),
với \(d\) được tính bằng xentimet, ta quy ước rằng \(d > 0\) khi vật ở phía trên vị trí cân bằng, \(d < 0\) khi vật ở phía dưới vị trí cân bằng. Hỏi :
LG a
Ở thời điểm nào trong 1 giây đầu tiên, vật ở vị trí cân bằng ?
Lời giải chi tiết:
Ta có:\(d=5\sin 6t - 4cos6t\) \( = \sqrt {41} \left( {{5 \over {\sqrt {41} }}\sin 6t - {4 \over {\sqrt {41} }}\cos 6t} \right) \) \(= \sqrt {41} \sin \left( {6t - \alpha } \right)\)
trong đó số \(α\) được chọn sao cho \(\cos \alpha = {5 \over {\sqrt {41} }}\,\text{ và }\,\sin \alpha = {4 \over {\sqrt {41} .}}\)
Sử dụng bảng số hoặc máy tính bỏ túi, ta chọn được \(α ≈ 0,675\).
Vật ở vị trí cân bằng khi \(d = 0\), nghĩa là \(\sin(6t – α) = 0\)
\( \Leftrightarrow t = {\alpha \over 6} + k{\pi \over 6}\) (với \(k \in\mathbb Z\))
Ta cần tìm \(k\) nguyên dương sao cho \(0 ≤ t ≤ 1\)
\(0 ≤ t ≤ 1\) \( ⇔ 0 \le {\alpha \over 6} + k{\pi \over 6} \le 1 \) \(\Leftrightarrow - {\alpha \over \pi } \le k \le {{6 - \alpha } \over \pi }\)
Với \(α ≈ 0,675\), ta thu được \(-0,215 < k < 1,7\), nghĩa là \(k\in \{0;1\}\).
Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở vị trí cân bằng là :
\(t \approx {\alpha \over 6} \approx 0,11\) (giây) và \(t = {\alpha \over 6} + {\pi \over 6} \approx 0,64\) (giây)
LG b
Ở thời điểm nào trong 1 giây đầu tiên, vật ở xa vị trí cân bằng nhất ?
(Tính chính xác đến \({1 \over {100}}\) giây).
Lời giải chi tiết:
Vật ở xa vị trí cân bằng nhất khi và chỉ khi \(|d|\) nhận giá trị lớn nhất.
Điều đó xảy ra nếu \(\sin(6t – α) = ± 1\). Ta có :
\(\sin \left( {6t - \alpha } \right) = \pm 1 \)
\(\Leftrightarrow \cos \left( {6t - \alpha } \right) = 0 \)
\(\Leftrightarrow t= {\alpha \over 6} + {\pi \over {12}} + k{\pi \over 6}\)
Ta tìm k nguyên dương sao cho \(0 ≤ t ≤ 1\)
\(\eqalign{
& 0 \le t \le 1 \Leftrightarrow 0 \le {\alpha \over 6} + {\pi \over {12}} + k{\pi \over 6} \le 1 \cr
& \Leftrightarrow - {\alpha \over \pi } - {1 \over 2} \le k \le {{6 - \alpha } \over \pi } - {1 \over 2} \cr} \)
Với \(α ≈ 0,675\), ta thu được \(-0,715 < k < 1,2\); nghĩa là \(k \in {\rm{\{ }}0;1\} \). Vậy trong khoảng 1 giây đầu tiên, có hai thời điểm vật ở xa vị trí cân bằng nhất là :
\(t = {\alpha \over 6} + {\pi \over {12}} \approx 0,37\,\left( {s} \right)\) và \(t = {\alpha \over 6} + {\pi \over {12}} + {\pi \over 6} \approx 0,90\,\left( \text{s} \right)\)

