Đề bài
Cho tứ diện ABCD. Bốn điểm P, Q, R, S lần lượt nằm trên bốn cạnh AB, BC, CD, DA và không trùng với các đỉnh của tứ diện. Chứng minh rằng
a. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PQ, RS, AC hoặc đôi một song song hoặc đồng quy
b. Bốn điểm P, Q, R, S đồng phẳng khi và chỉ khi ba đường thẳng PS, RQ, BD hoặc đôi một song song hoặc đồng quy
Lời giải chi tiết
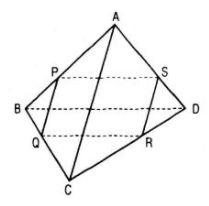
a. Nếu P, Q, R, S đồng phẳng thì chúng cùng thuộc mặt phẳng (PQRS).
Ta có:
(PQRS) ∩ (ABC) = PQ
(PQRS) ∩ (ACD) = RS
(ABC) ∩ (ACD) = AC
Theo định lí về giao tuyến của ba mặt phẳng thì PQ, SR, AC hoặc đôi một song song hoặc đồng quy.
Ngược lại, nếu ba đường thẳng PQ, AC, RS hoặc đôi một song song hoặc đồng quy thì hai đường thẳng PQ và RS cùng thuộc một mặt phẳng, từ đó bốn điểm P, Q, R, S đồng phẳng.
b. Nếu P, Q, R, S đồng phẳng thì chúng cùng thuộc mặt phẳng (PQRS).
Ta có:
(PQRS) ∩ (ABD) = PS
(PQRS) ∩ (BCD) = RQ
(ABD) ∩ (BCD) = BD
Theo định lí về giao tuyến của ba mặt phẳng thì PS, RQ, BD hoặc đôi một song song hoặc đồng quy.
Ngược lại, nếu ba đường thẳng PS, RQ, BD hoặc đôi một song song hoặc đồng quy thì hai đường thẳng PS và RQ cùng thuộc một mặt phẳng, từ đó bốn điểm P, Q, R, S đồng phẳng.

