Đề bài
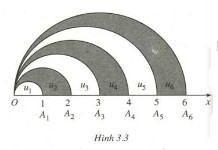
Trên tia Ox lấy các điểm A1, A2, …, An, … sao cho với mỗi số nguyên dương n, OAn = n. Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính OAn, n = 1, 2, … . Kí hiệu u1 là diện tích của nửa hình tròn đường kính OA1 và với mỗi n ≥ 2, kí hiệu un là diện tích của hình giới hạn bởi nửa đường tròn đường kính OAn – 1 , nửa đường tròn đường kính OAn và tia Ox (h 3.3). Chứng minh rằng dãy số (un) là một cấp số cộng. Hãy xác định công sai của cấp số cộng đó.
Lời giải chi tiết
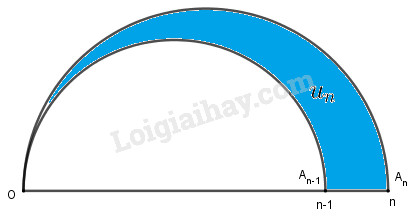
Với \(n ≥ 2\) ta có :
Diện tích nửa đường tròn đường kính \(OA_n\) là: \({S_n} = \frac{1}{2}\pi .{\left( {\frac{{O{A_n}}}{2}} \right)^2} = \frac{1}{8}\pi {n^2}\)
Diện tích nửa đường tròn đường kính \(OA_{n-1}\) là: \({S_{n-1}} = \frac{1}{2}\pi .{\left( {\frac{{O{A_{n-1}}}}{2}} \right)^2} = \frac{1}{8}\pi {(n-1)^2}\)
Do đó,
\(\eqalign{
& {u_n} ={S_n} - {S_{n-1}}\cr& = \frac{1}{8}\pi {n^2} - \frac{1}{8}\pi {\left( {n - 1} \right)^2} \cr
& = {1 \over 8}\pi \left[ {\left( {{n^2} - {{\left( {n - 1} \right)}^2}} \right)} \right] \cr
& = \frac{1}{8}\pi \left( {{n^2} - {n^2} + 2n - 1} \right)\cr&= {{\left( {2n - 1} \right)\pi } \over 8}\,\left( {n \ge 2} \right) \cr
& \Rightarrow {u_{n + 1}} - {u_n} \cr&= {{2n + 1} \over 8}\pi - {{\left( {2n - 1} \right)} \over 8}\pi \cr&= {\pi \over 4},\forall n \ge 2 \cr} \)
Mặt khác
\({u_2} - {u_1} = {{3\pi } \over 8} - {\pi \over 8} = {\pi \over 4}\)
Vậy \({u_{n + 1}} - {u_n} = {\pi \over 4}\;\forall n \in\mathbb N^*\)
Do đó (un) là cấp số cộng với công sai \(d = {\pi \over 4}.\)

