Đề bài
Cho hình chóp S.ABC. Lấy các điểm A’, B’, C’ lần lượt thuộc các tia SA, SB, SC sao cho SA = aSA’, SB = bSB’, SC = cSC’, trong đó a, b, c là các số thay đổi. Chứng minh rằng mặt phẳng (A’B’C’) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.
Lời giải chi tiết
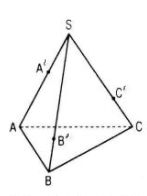
Ta có: \(\overrightarrow {SA} = a\overrightarrow {SA'} ,\;\overrightarrow {SB} = b\overrightarrow {SB'} ,\;\overrightarrow {SC} = c\overrightarrow {SC} .\)
Gọi G là trọng tâm của tam giác ABC thì
\(\eqalign{ & \overrightarrow {SG} = {1 \over 3}.\left( {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} } \right) \cr & Vay\,\overrightarrow {SG} = {a \over 3}\overrightarrow {SA'} + {b \over 3}\overrightarrow {SB'} + {c \over 3}\overrightarrow {SC'} \cr} \)
Mặt phẳng (A’B’C’) đi qua G khi và chỉ khi 4 điểm G, A’, B’, C’ đồng phẳng, nên theo kết quả bài tập 5 (SGK trang 91) , điều đó xảy ra nếu và chỉ nếu \({a \over 3} + {b \over 3} + {c \over 3} = 1\) , tức là: a + b + c = 3.

