Đề bài
Cho tứ diện ABCD. Gọi M, N là hai điểm phân biệt cùng thuộc đường thẳng AB; P, Q là hai điểm phân biệt cùng thuộc đường thẳng CD. Xét vị trí tương đối của hai đường thẳng MQ, NP và vị trí tương đối của hai đường thẳng MP, NQ
Lời giải chi tiết
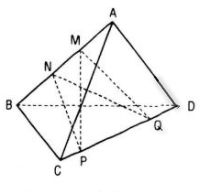
Hai đường thẳng MQ và NP chéo nhau.
Thật vậy, giả sử chúng không chéo nhau, tức chúng cùng thuộc một mp(\(\alpha\)) nào đó. Vậy M, N, P, Q cùng thuộc mp(\(\alpha\)) và do đó A, B, C, D cùng thuộc mp(\(\alpha\)). Điều này mâu thuẫn với giả thiết ABCD là một tứ diện.
Chứng minh tương tự, hai đường thẳng MP và NQ cũng chéo nhau.

