Đề bài
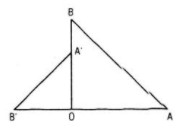
Cho hai tam giác vuông cân OAB và OA'B' có chung đỉnh O sao cho O nằm trên đoạn thẳng AB' và nằm ngoài đoạn thẳng A'B (h.16). Gọi G và G' lần lượt là trọng tâm các tam giác OAA' và OBB'.Chứng minh GOG' là tam giác vuông cân.
Lời giải chi tiết
Gọi Q là phép quay tâm O, góc quay \({\pi \over 2}\) (bằng góc lượng giác (OA ; OB)).
Khi đó Q:
+) biến O thành O
+) biến A thành B
+) biến A’ thành B’
Tức là Q biến tam giác OAA’ và OBB’
Bởi vậy Q biến G (trọng tâm tam giác OAA’) thành G’ (trọng tâm tam giác OBB’).
Suy ra \(OG = OG’\) và \(\widehat {GOG'} = {\pi \over 2}\)
Vậy GOG’ là tam giác vuông cân tại đỉnh O
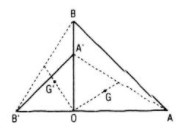
Chú ý: Phép quay Q biến trọng tâm G tam giác ABC thành trọng tâm G’ của tam giác A’B’C’ ảnh của △ABC qua Q được suy ra từ phép quay Q biến trung điểm của đoạn thẳng thành trung điểm đoạn thẳng.
Nghĩa là do phép quay Q biến AA' thành BB' thì biến trung điểm M của AA' thành trung điểm N của BB'.
Do đó Q biến OM thành ON. Khi đó Q biến G (thuộc OM) thành G' (thuộc ON) và \(OG' = OG = \frac{2}{3}OM = \frac{2}{3}ON\).
Vậy Q biến G thành G' là trọng tâm tam giác OBB'.

