Lựa chọn câu để xem lời giải nhanh hơn
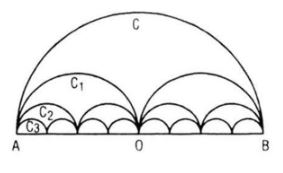
Gọi C là nửa đường tròn đường kính AB = 2R, C1 là đường gồm hai nửa đường tròn đường kính \({{AB} \over 2}\), C2 là đường gồm bốn nửa đường tròn đường kính \({{AB} \over 4},...\) Cn là đường gồm \({2^n}\) nửa đường tròn đường kính \({{AB} \over {{2^n}}},...\). Gọi pn là độ dài của Cn, Sn là diện tích hình phẳng giới hạn bởi Cn và đoạn thẳng AB.
LG a
Tính pn và Sn.
Phương pháp giải:
Sử dụng công thức tính chu vi và diện tích hình tròn:
+) Chu vi \(2\pi R\).
+) Diện tích \(\pi {R^2}\).
Lời giải chi tiết:

LG b
Tìm giới hạn của các dãy số (pn) và (Sn).
Lời giải chi tiết:
\(\begin{array}{l}
\lim {p_n} = \lim \pi R = \pi R\\
\lim {S_n} = \lim \dfrac{{\pi {R^2}}}{{{2^{n + 1}}}} = 0
\end{array}\)