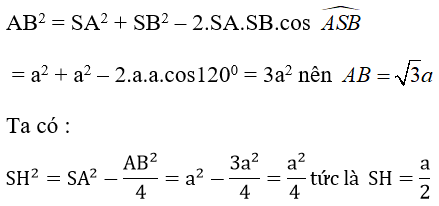Đề bài
Cho hình chóp S.ABC có SA = SB = SC = a, \(\widehat {ASB} = 120^\circ ,\widehat {BSC} = 60^\circ ,\widehat {CSA} = 90^\circ \) .
a. Chứng tỏ rằng ABC là tam giác vuông
b. Tính khoảng cách từ S đến mặt phẳng (ABC)
Lời giải chi tiết
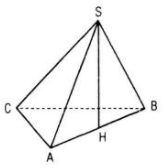
a. Ta có:
\(\eqalign{ & \overrightarrow {CA} .\overrightarrow {CB} \cr &= \left( {\overrightarrow {SA} - \overrightarrow {SC} } \right)\left( {\overrightarrow {SB} - \overrightarrow {SC} } \right) \cr & = \overrightarrow {SA} .\overrightarrow {SB} - \overrightarrow {SA} .\overrightarrow {SC} - \overrightarrow {SC} .\overrightarrow {SB} + S{C^2} \cr & = {a^2}\cos 120^\circ - {a^2}\cos 90^\circ - {a^2}\cos 60^\circ + {a^2} \cr & = {a^2} - {{{a^2}} \over 2} - {{{a^2}} \over 2} = 0 \cr & \Rightarrow CA \bot CB \cr} \)
⇒ ΔABC vuông tại C.
b. Kẻ SH ⊥ mp(ABC), do SA = SB = SC nên HA = HB = HC mà ΔABC vuông tại C nên H là trung điểm của AB.
Áp dụng định lí cô sin vào tam giác ABC, ta có: