Cho hình hộp chữ nhật ABCD.A’B’C’D’ có AB = AA’ = a, AC’ = 2a.
LG a
Tính khoảng cách từ điểm D đến mặt phẳng (ACD’)
Giải chi tiết:
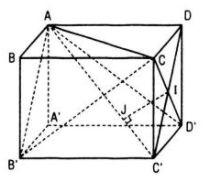
a. Xét tứ diện DACD’ có DA, DC, DD’ đôi một vuông góc nên khoảng cách DH từ D đến mặt phẳng (ACD’) được tính bởi hệ thức :
\({1 \over {D{H^2}}} = {1 \over {D{A^2}}} + {1 \over {D{C^2}}} + {1 \over {DD{'^2}}}\)
Ta có: DC = a. DD’ = a
\(AC{'^2} = A{C^2} + CC{'^2} = D{A^2} + D{C^2} + CC{'^2}\)
Hay \(4{a^2} = D{A^2} + {a^2} + {a^2},\)tức là \(D{A^2} = 2{a^2}\)
Vậy \({1 \over {D{H^2}}} = {1 \over {2{a^2}}} + {1 \over {{a^2}}} + {1 \over {{a^2}}} = {5 \over {2{a^2}}}\)
Do đó : \(DH = {{a\sqrt {10} } \over 5}\)
LG b
Tìm đường vuông góc chung của các đường thẳng AC’ và CD’. Tính khoảng cách giữa hai đường thẳng ấy.
Giải chi tiết:
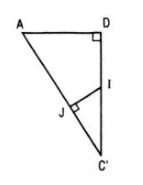
Vì CD = DD’ = a nên CD’ ⊥ C’D. Mặt khác AD ⊥ (CDD’C’) nên CD’ ⊥ AC’ và CD’ ⊥ mp(AC’D). Gọi giao điểm của CD’ với mp(AC’D) là I. Trong mp(AC’D) kẻ IJ vuông góc với AC’ tại J thì IJ là đường vuông góc chung của AC’ và CD’.
Ta tính khoảng cách giữa AC’ và CD’
Ta có: ΔC’JI đồng dạng ΔC’DA nên \({{IJ} \over {AD}} = {{IC'} \over {AC'}}\)
Suy ra : \(IJ = AD.{{C'D} \over {2AC'}}\)
Mặt khác \(C'D = a\sqrt 2 \) nên \(IJ = a\sqrt 2 .{{a\sqrt 2 } \over {2.2a}} = {a \over 2}\)

