a. Vẽ đồ thị của hàm số \(y = \sin x\) rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng \((-π ; 4π)\) là nghiệm của mỗi phương trình sau :
1. \(\sin x = - {{\sqrt 3 } \over 2}\)
2. \(\sin x = 1\)
b. Cũng câu hỏi tương tự cho hàm số \(y = \cos x\) đối với mỗi phương trình sau
1. \(\cos x = {1 \over 2}\)
2. \(\cos x = -1\).
LG a
Vẽ đồ thị của hàm số \(y = \sin x\) rồi chỉ ra trên đồ thị đó các điểm có hoành độ thuộc khoảng \((-π ; 4π)\) là nghiệm của mỗi phương trình sau :
1. \(\sin x = - {{\sqrt 3 } \over 2}\)
2. \(\sin x = 1\)
Lời giải chi tiết:
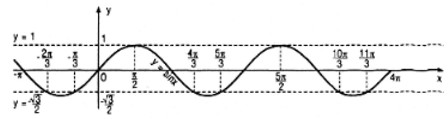
\(1/\,\sin x = - {{\sqrt 3 } \over 2} \)
Vẽ đường thẳng (d): \(y = - {{\sqrt 3 } \over 2}\).
Ta thấy trong khoảng \((-π ; 4π)\) thì (d) cắt đồ thị hàm số \(y=\sin x\) tại các điểm có hoành độ:
\({x_1} = - {\pi \over 3};{x_2} = {{5\pi } \over 3};{x_3} = {{11\pi } \over 3}\); \({x_4} = - {{2\pi } \over 3};{x_5} = {{4\pi } \over 3};{x_6} = {{10\pi } \over 3}\).
Kiểm tra bằng cách đại số:
\(\begin{array}{l}
\sin x = - \frac{{\sqrt 3 }}{2} = \sin \left( { - \frac{\pi }{3}} \right)\\
\Leftrightarrow \left[ \begin{array}{l}
x = - \frac{\pi }{3} + k2\pi \\
x = \pi - \left( { - \frac{\pi }{3}} \right) + k2\pi
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = - \frac{\pi }{3} + k2\pi \\
x = \frac{{4\pi }}{3} + k2\pi
\end{array} \right.
\end{array}\)
*Với \(x = - {\pi \over 3} + k2\pi \,\text{ và }\,x \in \left( { - \pi ;4\pi } \right)\) ta có nghiệm :
\({x_1} = - {\pi \over 3};{x_2} = {{5\pi } \over 3};{x_3} = {{11\pi } \over 3}\)
* Với \(x = {{4\pi } \over 3} + k2\pi \,\text{ và }\,x \in \left( { - \pi ;4\pi } \right)\) ta có nghiệm :
\({x_4} = - {{2\pi } \over 3};{x_5} = {{4\pi } \over 3};{x_6} = {{10\pi } \over 3}\)
2/ \(\sin x = 1 \Leftrightarrow x = {\pi \over 2} + k2\pi \)
Vẽ đường thẳng \(d_2:y=1\).
Trong khoảng \((-\pi;4\pi)\) thì \(d_2\) cắt đồ thị hàm số \(y=\sin x\) tại hai điểm phân biệt có hoành độ là:
\({x_1} = {\pi \over 2};{x_2} = {{5\pi } \over 2}.\)
Kiểm tra lại bằng cách đại số:
* Với \(x = {\pi \over 2} + k2\pi \,\text{và}\,x \in \left( { - \pi ;4\pi } \right)\) ta có nghiệm :
\({x_1} = {\pi \over 2};{x_2} = {{5\pi } \over 2}.\)
LG b
Cũng câu hỏi tương tự cho hàm số \(y = \cos x\) đối với mỗi phương trình sau
1. \(\cos x = {1 \over 2}\)
2. \(\cos x = -1\).
Lời giải chi tiết:
Tương tự câu a) ta có hình vẽ sau :
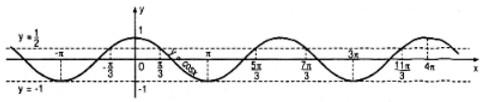
1. Nghiệm của phương trình \(\cos x = {1 \over 2}\) thuộc khoảng \((-π;4π)\) là :
\({x_1} = - {\pi \over 3};{x_2} = {\pi \over 3};{x_3} = {{5\pi } \over 3};\)
\({x_4} = {{7\pi } \over 3};{x_5} = {{11\pi } \over 3}\)
2. Nghiệm của phương trình \(\cos x = -1\) thuộc khoảng \((-π ; 4π)\) là :
\(x_1= -π\), \(x_2 = π\), \(x_3= 3π\)

